Таблиця 2

+	.	.	.	+
.	+	.	.	+
.	.	+	.	+
.	.	.	+	+
+	+	+	+	+

 

Методом розріджених матриць називають метод рішення СЛАР на основі методу Гауса з урахуванням розрідженості (первинної й вторинної) матриці коефіцієнтів.

Метод розріджених матриць можна реалізувати шляхом інтерпретації й компіляції. В обох випадках створюються масиви ненульових коефіцієнтів матриці (з урахуванням вторинних ненулів) і масиви координат цих ненульових елементів.

При цьому виграш у витратах пам’яті досить значний. Так, при матриці помірного розміру 200х200 без урахування розрідженості буде потрібно 320 кбайт. Якщо ж взяти характерне значення 9 для середнього числа ненулів в одному рядку, то для коефіцієнтів і покажчиків координат буде потрібно не більше 28 кбайт.

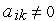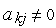У випадку інтерпретації моделююча програма для кожної операції по (3.17) при й знаходить, використовуючи покажчики, потрібні коефіцієнти й виконує арифметичні операції по (3.17). Оскільки СЛАР в процесі аналізу вирішується багаторазово, те й операції пошуку потрібних коефіцієнтів також повторюються багаторазово, на що природно витрачається машинний час.

Спосіб компіляції більше економічний по витратах часу, але уступає способу інтерпретації по витратах пам’яті. При компіляції пошук потрібних для (3.17) коефіцієнтів виконується однократно перед чисельним рішенням задачі. Замість безпосереднього виконання арифметичних операцій для кожної з них компілюється команда зі знайденими адресами ненульових коефіцієнтів. Такі команди утворять робочу програму рішення СЛАР, що і буде вирішуватися багаторазово. Очевидно, що тепер у робочій програмі буде виконуватися мінімально необхідне число арифметичних операцій.

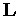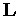До числа різновидів методу Гауса відноситься метод LU-розкладання, що заснований на розкладанні матриці коефіцієнтів системи (3.16) на верхні й нижню трикутні матриці, що еквівалентно прямому ходу в методі Гауса. Елементи матриць і обчислюються по рекурентним формулам

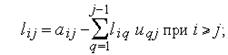
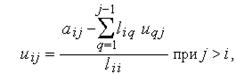
причому 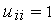, , 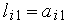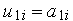. Стовпці матриці 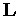обчислюються в порядку збільшення 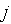, починаючи c 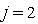. Після обчислення 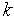-го стовпця 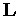безпосередньо виконується розрахунок 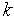-го рядка . Зворотний хід полягає в розрахунку вектора 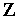з матричного рівняння 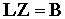й, нарешті, вектора 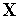з рівняння .

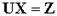Крім методу Гауса, для рішення систем лінійних алгебраїчних рівнянь (3.17) застосовують ітераційні методи: метод простої ітерації, метод Зейделя, метод Якобі, методи послідовних верхньої й нижньої релаксації. Наприклад, у методі простої ітерації обчислення виконують по формулі

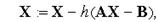
причому для забезпечення збіжності параметр потрібно вибирати з умови 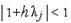для будь-якого 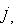де 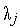— 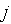-е власне значення матриці .