Параболоиды.
Определение 10.4. Параболоидаминазываются поверхности, которые в некоторой системе прямоугольных декартовых координат определяются каноническими уравнениями
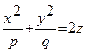 , (10.5)
, (10.5)
 , (10.6)
, (10.6)
где p и q - положительные числа, называемые параметрами параболоида. Параболоид, определяемый уравнением (10.5), называется эллиптическим. Сечения эллиптического параболоида, параллельные оси Oz - параболы; сечения, параллельные плоскости xOy - эллипсы. Параболоид, определяемый уравнением (10.6), называется гиперболическим. Сечения гиперболического параболоида, параллельные плоскостям yOz и xOz - параболы; сечения, параллельные плоскости xOy - гиперболы.
Замечание. В случае, когда p = q, эллиптический параболоид (10.5) является поверхностью вращения (вокруг оси Oz).
Пример. Определить вид поверхности
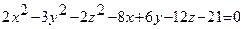 ,
,
используя метод сечения плоскостями.
Решение. Уравнение поверхности не содержит членов с произведением координат, следовательно плоскости симметрий параллельны координатным плоскостям.
Пересекая поверхность плоскостями 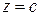 параллельными плоскости xOy, получим:
параллельными плоскости xOy, получим:
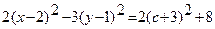 .
.
Так как 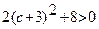 для любого с, полученная кривая является гиперболой с действительной осью, параллельной оси Ox.
для любого с, полученная кривая является гиперболой с действительной осью, параллельной оси Ox.
Пересекая поверхность плоскостями  аналогично получаем уравнение
аналогично получаем уравнение
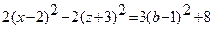
гиперболы с действительной осью, параллельной оси Ox.
При пересечении данной поверхности плоскостями 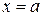 , параллельными координатной плоскости yOz, получаем:
, параллельными координатной плоскости yOz, получаем:
 .
.
Последнее уравнение при  ,т.е. при
,т.е. при  и
и 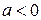 , есть уравнение эллипса.
, есть уравнение эллипса.
Таким образом сечениями поверхности плоскостями являются эллипсы и гиперболы, действительные оси которых параллельны. Следовательно, исследуемая поверхность - двуполостный гиперболоид. Его уравнение можно преобразовать к каноническому виду:
 .
.