Строение и виды теорем
Теорема – это высказывание, истинность которого устанавливается посредством рассуждения (доказательства).
С логической точки зрения теорема представляет собой высказывание вида А Þ В , где А и В – предикаты с одной или несколькими переменными. Предложение А называют условием теоремы, а предложение В – ее заключением.
Рассмотрим теорему: «Если натуральное число делится на 2 и на 3, то оно делится на 6». Условие теоремы: «число делится на 2 и на 3», заключение теоремы: «число делится на 6». Условие и заключение теоремы представляют собой предикаты, заданные на множестве Х натуральных чисел. Данное предложение истинно при всех х из множества Х, следовательно, запись теоремы будет следующей: (" х Î Х) А (х) Þ В (х).
Т.о. в записи теоремы можно выделить 3 части:
1) разъяснительную (" х Î Х) – в ней описываются множества объектов, о которых идет речь в теореме;
2) условие теоремы: предикат А (х), заданный на множестве Х;
3) заключение теоремы: предикат В (х), заданный на множестве Х.
Для всякой теоремы вида (" х Î Х) А (х) Þ В (х) можно сформулировать предложения:
обратное данному (" х Î Х) В (х) Þ А (х),
противоположное данному (" х Î Х) 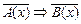 ,
,
обратное противоположное данному (" х Î Х) 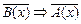 .
.
Заметим, что эти предложения не всегда является теоремами. Например, предложение, обратное для теоремы «если каждое слагаемое делится на данное число, то и сумма делится на данное число» будет ложным. Оно будет формулироваться так: «Если сумма делится на данное число, то и каждое слагаемое делится на данное число». Чтобы убедиться в том, что оно ложное, можно привести контрпример: 3 + 7 = 10. Сумма 10 делится на 5, но ни одно слагаемое на 5 не делится. Данные предложения будут теоремами только в том случае, если они истинны.
Пример. Рассмотрим предложение: «Если каждое слагаемое – четное число, то и сумма – четное число». В нашем примере предикат А (х): «каждое слагаемое – четное число», В (х): «сумма – четное число». Данное предложение является истинным, поэтому его можно назвать теоремой.
Построим обратное предложение: «Если сумма – четное число, то и каждое слагаемое – четное число». Оно ложное, т.к. можно привести контрпример 8 = 5 + 3.
Противоположное предложение: «Если хотя бы одно из слагаемых – нечетное число, то и сумма – нечетное число. Оно также ложно (можно воспользоваться тем же контрпримером).
Обратное противоположному предложение: «Если сумма – нечетное число, то хотя бы одно слагаемое – нечетное число». Оно истинно, поэтому оно также является теоремой.
Заметим, что прямое и обратное противоположному предложения всегда имеют одинаковые значения истинности, т.к. имеется равносильность (А Þ В) Û (В Þ А), называемая законом контрапозиции. Из этого предложения также следует, что предложения, обратное данному и противоположное данному также имеют одинаковые значения истинности. Поэтому, рассматривая их, достаточно доказать (или опровергнуть) какое-нибудь одно, тем самым будет доказано (или опровергнуто) другое.
Если для данное теоремы А (х) Þ В (х) существует обратная В (х) Þ А (х), то их можно соединить в одну А (х) Û В (х), в формулировке которой будут использоваться слова «необходимо и достаточно», «тогда и только тогда».
Заметим также, что если условие или заключение теоремы представляет собой конъюнкцию или дизъюнкцию, то, чтобы получить предложение, противоположное данному, нужно учитывать правила построения отрицания конъюнкции или дизъюнкции.