ЛОКАЛЬНАЯ И ИНТЕГРАЛЬНАЯ ТЕОРЕМА ЛАПЛАСА
8.1 Локальная теорема Лапласа
Вероятность того, что в n независимых испытаниях, в каждом из которых вероятность появления события равна
р (0 < p < 1), событие наступит ровно k раз (безразлично, в какой последовательности), приближенно равна (тем точнее, чем больше n)
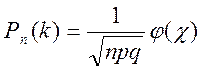
где
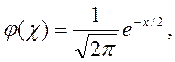
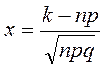
Таблица функции φ (x) для положительных значений х приведена в приложении 1; для отрицательных значений х пользуются этой же таблицей [функция φ (x) четная, следовательно, φ ( - x) = φ (x)].
8.2 Интегральная теорема Лапласа. Вероятность того, что в n независимых событиях, в каждом из которых вероятность появления события равна p(0<p<1), событие наступит не менее k1 раз и не более k2 раз, приближенно равна
Р(k1 ;k2 ) = Ф( х") – Ф( х' ),
где
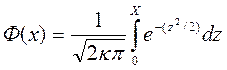 - функция Лапласа,
- функция Лапласа,
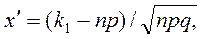

Таблица функции Лапласа для положительных значений
0 ≤ х ≤ 5 приведена в приложении 2; для значений x>5 полагают Ф(х) = 0,5. Для отрицательных значений х используют эту же таблицу, учитывая что функция Лапласа нечетная [Ф(-х) = - Ф(х)].
Задача 15.Найти вероятность того, что событие А наступит 1100 раз в 2500 испытаниях, если вероятность появления этого события в каждом испытании равна 0,5.
Решение. Так как n велико, воспользуемся локальной теоремой Лапласа

Вычислим х:
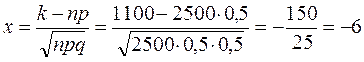
 Функция
Функция 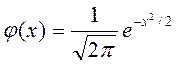 - четная, поэтому φ (-6) = φ (6) = 0
- четная, поэтому φ (-6) = φ (6) = 0
По таблице приложения 1 найдем φ (6) = 0.
Искомая вероятность
Р2500 (1100) = 1/25 ∙0 = 0.
Ответ: Вероятность того, что событие А наступит 1100 раз в 2500 испытаниях, равна нулю.
Задача 16. Вероятность появления события в каждом из 100 независимых испытаний постоянна и равна р = 0,6. Найти вероятность того, что событие появится: а) не менее 55 раз и не более 80 раз; б) не менее 55 раз
Решение. Воспользуемся интегральной теоремой Лапласа:
Р(k1 ;k2 ) = Ф( х") – Ф( х' ),
где Ф(х) – функция Лапласа,
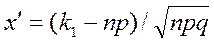 ,
, 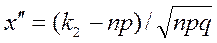 .
.
а) По условию, n = 100; р = 0,6; q = 0,4; k1 = 55; k2 = 80.
Вычислим x' и х":
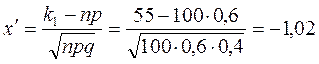

Учитывая, что функция Лапласа нечетная, т.е. Ф(-х) = - Ф(х), получим:
Р100 (55; 80) = Ф(4,08) – Ф(- 1,02) = Ф(4,08) + Ф(1,02).
По таблице приложения 2 найдем
Ф(4,08) = 0,4999; Ф(1,02) = 0,3461.
Искомая вероятность
Р100 (55; 80) = 0,4999 + 0,3461 = 0,846.
б) Требование, чтобы событие появилось не менее 55 раз, означает, что число появлений события может быть равно 55, либо 56, …, либо 100. Таким образом, в рассматриваемом случае следует принять k1 = 55, k2 = 100. Тогда,
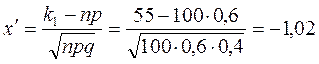

По таблице приложения 2 найдем Ф; Ф(8,17) = 0,5.
Искомая вероятность
Р100 (55; 80) = Ф(8,17) – Ф(- 1,02) = 0,5 + 0,3461 = 0,8461.
Ответ: а) Вероятность того, что событие появится не менее 55 раз и не более 80 раз, равна 0,846;
б) Вероятность того, что событие появится не менее 55 раз, равна 0,8461.
9. ВЕРОЯТНОСТЬ ОТКЛОНЕНИЯ ОТНОСИТЕЛЬНОЙ ЧАСТОТЫ ОТ ТЕОРЕТИЧЕСКОЙ ВЕРОЯТНОСТИ
Вероятность того, что в n независимых испытаниях отклонение относительной частоты  появления некоторого события A от вероятности его появления p по абсолютной величине не больше заданного числа ε>0, т.е. вероятность осуществления неравенства:
появления некоторого события A от вероятности его появления p по абсолютной величине не больше заданного числа ε>0, т.е. вероятность осуществления неравенства:

 , приближенно равна удвоенной функции Лапласа при Х=
, приближенно равна удвоенной функции Лапласа при Х=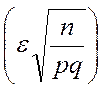 .
.
P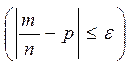 = 2Φ
= 2Φ .
.
Задача 17. Вероятность появления события в каждом из 625 независимых испытаний равна 0,8. Найти вероятность того, что относительная частота появления события отклонится от его вероятности по абсолютной величине не более чем на 0,04.
Решение. По условию n=625; p=0,8; q=0,2; ε=0,04. Требуется найти вероятность P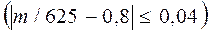 . Воспользуемся формулой
. Воспользуемся формулой
P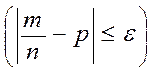 = 2Φ
= 2Φ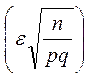 .
.
Имеем:
P =2Φ
=2Φ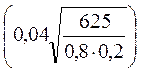 =2Φ(2,5).
=2Φ(2,5).
По таблице приложения 2 найдем Φ(2,5)=0,4938. Следовательно, 2Φ(2,5)= 2•0,4938=0,9876. Итак, искомая вероятность приближенно равна 0,9876.