Следствия из свойств
1о Необходимым и достаточным условием перпендикулярности векторов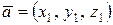 
и 
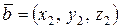является равенство
.
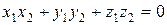20 Угол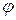 
между векторам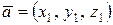и и 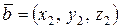определяется соотношением:
.
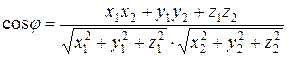3о Если некоторая ось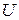 
составляет с координатными осями углы 
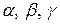, то проекция произвольного вектора 
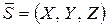на эту ось будет равна:
.
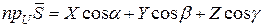4о Проекция вектора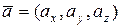 
на вектор 
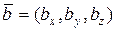находится по формуле:
.
Пример 3.1. Даны три точк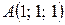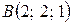и 
, 
и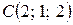 
. Найти угол a)
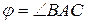; б) проекцию вектора 
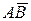на вектор 
.
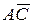Решение.
Найдем векторы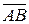 
и 
:
, 
.
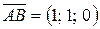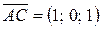a)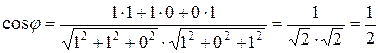 
.
Следовательно,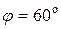 
.
б)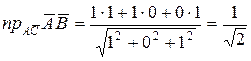 
.
Пример 3.2. Даны векторы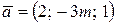 
и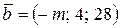 
. При каком значении 
эти векторы перпендикулярны?
Решение.
Из свойства 6о скалярного произведения векторов следует, что для того чтобы векторы 
и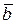 
были перпендикулярны, необходимо, чтобы 
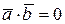. Найдем скалярное произведение векторов и :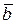
,
.
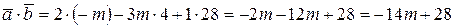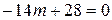Откуда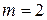 
.
Пример 3.3. Найти вектор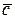 
, коллинеарный вектору 
и удовлетворяющий условию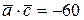 
.
Решение. Так как вектор 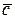коллинеарен вектору , то его координаты пропорциональны и могут быть следующими: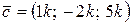 
. Тогда скалярное произведение этих векторов
,
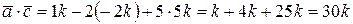а по условию 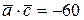, откуда
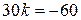, т.е. 
.
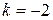Следовательно, координаты вектора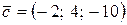 
.
Пример 3.4. Какой угол образуют единичные векторы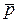 
и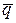 
, если векторы 
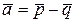и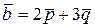 
взаимно перпендикулярны.
Решение.
Так как векторы и 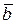взаимно перпендикулярны, то их скалярное произведение равно нулю, т.е.
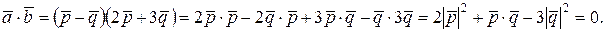
По условию задачи векторы 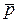и 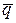единичные, т.е. 
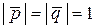, тогда последнее соотношение можно переписать иначе:
.
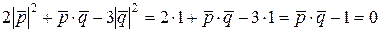Откуда
.
По формуле скалярного произведения двух векторов
,
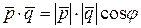где 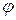– угол между векторам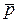и и 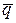. Тогда
.
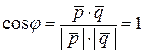Следовательно, угол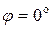 
(векторы коллинеарны).