Свойства векторного произведения
1о Векторное произведение 
на 
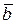есть вектор, обратный векторному произведению 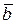на , т.е.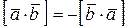 
.
2о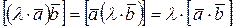 
– сочетательный закон.
3о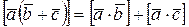 
; 
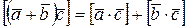– распределительный закон.
4о Векторное произведение двух векторов обращается в ноль тогда и только тогда, когда эти векторы коллинеарны.
Замечание. В частности, равно нулю и векторное произведение одинаковых множителей, т.е. 
. Поэтому понятие векторного квадрата не употребляется.
5о Если векторы и 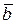приведены к общему началу, то модуль векторного произведения 
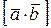равен площади параллелограмма, построенного на этих векторах, т.е. 
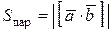, а площадь треугольника, построенного на векторах и 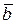, равна половине площади параллелограмма, т.е. 
.
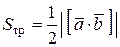6о Векторное произведение векторов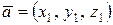 
и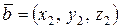 
определяется формулой:
.
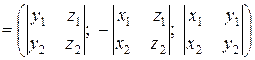Пример 4.1. Найти вектор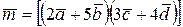 
, если известно, что 
; 
; 
; 
.
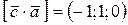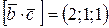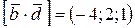Решение. Упростим:
Пример 4.2. Даны векторы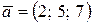 
и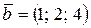 
. Найти координаты векторного произведения .
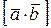Решение.
.
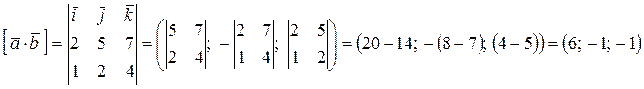Пример 4.3. Найти синус угла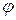 
между векторами 
и .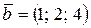
Решение. Из определения векторного произведения
.
Выразив отсюда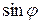 
, получим:
.
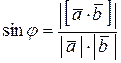Из примера 4.2.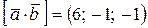 
, тогда
;
, 
.
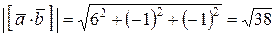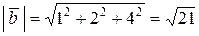Таким образом,
.
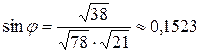Пример 4.4. В пространстве даны три точк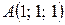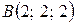и 
, 
и 
. Найти площадь 
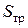треугольника 
.
Решение. Рассмотрим векторы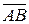 
и 
. Согласно 5о свойству векторного произведения, модуль векторного произведения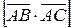 
, умноженный на 
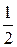равен площади треугольника, построенного на векторах 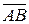и , т.е.
.
Найдем векторы 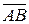и :
; 
.
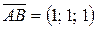Тогда
.
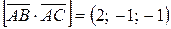
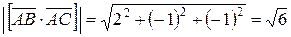Таким образом,
.