Свойства операций

1^о 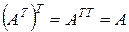, т.е. если над матрицей дважды произвести операцию транспонирования, то матрица останется неизменной.

Пример 2.6.На примере матрицы 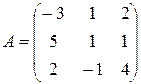, доказать, что .

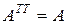Решение. Найдем матрицу , транспонированную по отношению к матрице :

.

После транспонирования последней матрицы, получим:

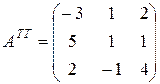, а это в точности есть матрица .

 

2^о 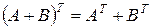, т.е. транспонированная матрица суммы двух матриц равна сумме транспонированных матриц.

Пример 2.7.Проверим это свойство для матриц 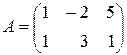и .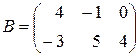

Решение.

Найдем матрицы, транспонированные по отношению к данным

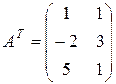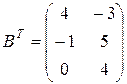; и их сумму .

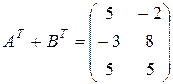Для того, чтобы проверить свойство 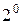, вычислим сумму исходных матриц, а затем транспонируем ее:

, .

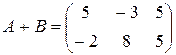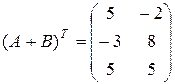Матрицы 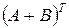и равны, что и требовалось доказать.

 

3^о 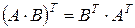, т.е. транспонированная матрица произведения двух матриц равна произведению транспонированных матриц, взятых в обратном порядке.

Пример 2.8. Проверим это свойство для матриц 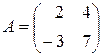и .

Решение.

Найдем произведение данных матриц:

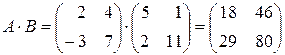
и запишем матрицу, транспонированную по отношению к ней:

.

Найдем произведение матриц, транспонированных по отношению к данным:

, , .

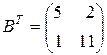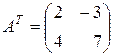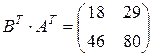Из полученного видно, что:.