Ранг матрицы
Векторы  ,
,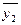 , …,
, …, 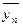 называются линейно зависимыми, если существуют такие действительные числа
называются линейно зависимыми, если существуют такие действительные числа 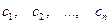 , одновременно не все равные нулю, что:
, одновременно не все равные нулю, что:
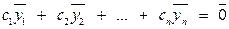 (5.1)
(5.1)
Векторы 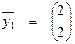 ,
, 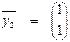 ,
, 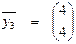 являются линейно зависимыми, т. к., например, для
являются линейно зависимыми, т. к., например, для 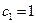 ,
, 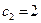 ,
,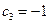 выполняется:
выполняется:
. 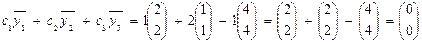
Векторы  ,
, 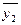 , …,
, …, 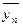 называются линейно независимыми, если (5.1)выполняется только при условии:
называются линейно независимыми, если (5.1)выполняется только при условии: 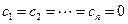 . Например, векторы
. Например, векторы  ,
, 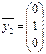 ,
, 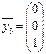 являются линейно независимыми, так как:
являются линейно независимыми, так как:
 ,
,
следовательно: 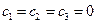 .
.
Несложно показать, что векторы вида: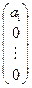 ,
,  , …,
, …,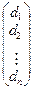 являются линейно независимыми.
являются линейно независимыми.
Квадратную матрицу А порядка n можно представить в виде совокупности n векторов:
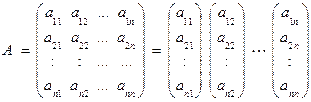
Рангом матрицы А rk A называется количество линейно независимых столбцов векторов этой матрицы (которое, кстати, всегда совпадает с количеством линейно независимых строк — векторов матрицы). Для нахождения ранга матрицы необходимо матрицу привести к треугольному виду, в котором все элементы, стоящие ниже главной диагонали, равны нулю. Для этого можно переставлять строки местами и прибавлять к элементам одной строки элементы другой строки, умноженные на одно и то же число. Тогда ранг матрицы будет равен количеству ненулевых строк в треугольной матрице.
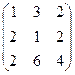
Пример. Найдем ранг матрицы А:
|
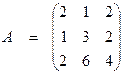
|
|
