Предел последовательности
Если каждому натуральному числу 1, 2, 3, …n, … поставим в соответствие действительное число  , то множество:
, то множество: 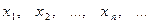 называется числовой последовательностью.
называется числовой последовательностью.
Числа 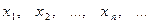 называются элементами последовательности. Сокращенно последовательность обозначают:
называются элементами последовательности. Сокращенно последовательность обозначают:  . Например:
. Например: 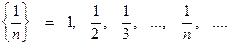 Произведением последовательности
Произведением последовательности 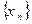 на число с называется последовательность
на число с называется последовательность  Суммой последовательностей {xn} и {yn} называется последовательность x1+y1, x2+y2, … yn+xn, … Произведением {xn} и {yn} называется последовательность
Суммой последовательностей {xn} и {yn} называется последовательность x1+y1, x2+y2, … yn+xn, … Произведением {xn} и {yn} называется последовательность  . Частным называется последовательность:
. Частным называется последовательность: 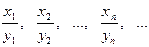 , если все элементы
, если все элементы 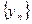 отличны от нуля.
отличны от нуля.
Число А называется пределом{xn}, если для любого сколь угодно малого положительного числа 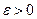 существует такой номер
существует такой номер  , что для всех последующих номеров
, что для всех последующих номеров  будет выполняться:
будет выполняться: 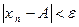 .
.
Обозначают: 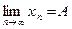 .
.
Геометрически это означает, что для любого малого 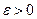 найдется такой номер
найдется такой номер  , что все элементы последовательности с номерами
, что все элементы последовательности с номерами  окажутся в отрезке
окажутся в отрезке 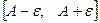 , причем в этом отрезке всегда будет находиться бесконечное число элементов последовательности, а за его границами — конечное число элементов.
, причем в этом отрезке всегда будет находиться бесконечное число элементов последовательности, а за его границами — конечное число элементов.

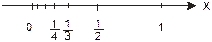 Например:
Например: 
Видно, что чем больше n, тем ближе элементы последовательности подходят к точке 0.
Для последовательности 0, 1, 0, 1,… предела не существует.
Число А, удовлетворяющее определению предела, является единственным.
Для{n}:  .
.
Свойства пределов последовательностей:
1. Предел суммы последовательностей равен сумме преде-лов последовательностей:
 .
.
2. Предел произведения последовательностей равен произведению пределов:
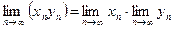 .
.
3. Предел частного равен частному пределов, при условии, что все элементы и предел знаменателя не равны 0:
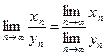 .
.
4.  , c = const.
, c = const.
Если предел одной или двух последовательностей равен бесконечности, то можно воспользоваться следующими соотношениями:
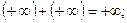
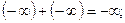

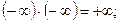 для
для 
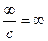 ,
,  ;
;  ;
;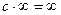 ,
, .
.
Если предел последовательности равен 0, то 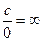 ,
,  .
.
При нахождении пределов могут возникнуть следующие неопределенности: 
Пример 1.Найдем предел:
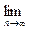
 .
.
Имеем неопределенность 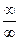 . Разделим числитель и знаменатель на n в наибольшей степени, которая имеется в знаменателе, т. е. на
. Разделим числитель и знаменатель на n в наибольшей степени, которая имеется в знаменателе, т. е. на  .
.
Получаем:  .
.
Вторым замечательным пределом называется предел:
 ,
,
е — есть константа.
Пример 2. Найдем 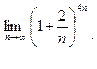
Имеем неопределенность 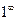 . Для ее раскрытия воспользуемся вторым замечательным пределом. Сделаем замену:
. Для ее раскрытия воспользуемся вторым замечательным пределом. Сделаем замену:  . Т. к.
. Т. к. 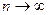 , то и
, то и  . Можно записать:
. Можно записать:
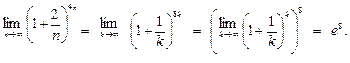
Пример 3.Найдем:
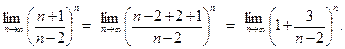
Сделаем замену:  . Следовательно,
. Следовательно, 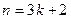 и
и  при
при 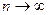 . Получаем:
. Получаем:
