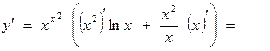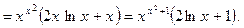Производная функции
Пусть функция 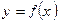 определена в точках
определена в точках 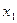 и
и 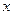 . Разность
. Разность 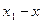 называется приращением аргумента, а
называется приращением аргумента, а 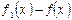 — приращением функции. Обозначают:
— приращением функции. Обозначают:  . Следовательно,
. Следовательно, 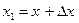 .
.
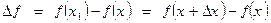 .
.
Пусть  определена в точке
определена в точке 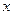 и в некоторой ее окрестности, такой, что
и в некоторой ее окрестности, такой, что 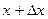 принадлежит этой окрестности.
принадлежит этой окрестности.
Функция 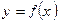 называется дифференцируемой в точке
называется дифференцируемой в точке 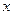 , если существует предел:
, если существует предел:
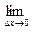
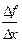 =
= 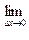
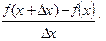
Этот предел называется производной функции 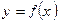 в точке
в точке 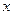 и обозначается:
и обозначается:
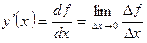 .
.
Для основных элементарных функций производные находят из определения производной. Справедливы следующие формулы дифференцирования:
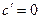 ,
, 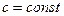 .
.
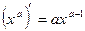 , в частности
, в частности 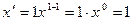 .
.
 ;
;  ;
;
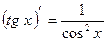 ;
; 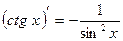 ;
;
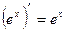 ;
; 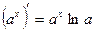 ;
;
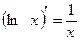 ;
; 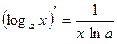 ;
;
 ;
; 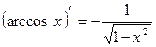 ;
;
 ;
; 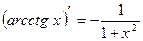 .
.
Используются следующие формулы дифференцирования. Если функции  и
и 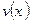 дифференцируемы, то
дифференцируемы, то
1. 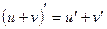 .
.
2. 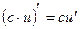 , где
, где 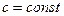 .
.
3. 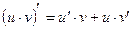 .
.
4. 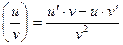 .
.
Если 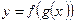 — сложная функция, причем функция
— сложная функция, причем функция  дифференцируема в точке
дифференцируема в точке 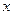 , а функция
, а функция 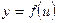 дифференцируема в точке
дифференцируема в точке 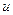 , тогда функция
, тогда функция 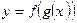 дифференцируема в точке
дифференцируема в точке 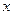 , причем:
, причем:
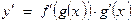 .
.
Пример 1. Найти производную функции: 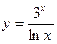 .
.
Используя правило 4 дифференцирования частного и формулы производных соответствующих функций, получим:
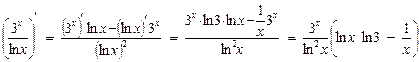 .
.
Пример 2. Найти производную:  . Здесь
. Здесь 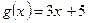 ;
;  .
.
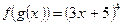 . Значит:
. Значит:

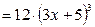 .
.
Если необходимо найти производную функции 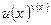 , то поступают следующим образом. Логарифмуют обе части равенст-ва:
, то поступают следующим образом. Логарифмуют обе части равенст-ва:  . Получим:
. Получим: 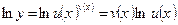 . Так как
. Так как 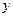 является функцией от
является функцией от 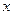 , то
, то  есть сложная функция, следовательно:
есть сложная функция, следовательно: 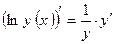 .
.
Таким образом, получаем:
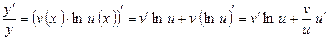 .
.
Значит: 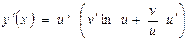 .
.
Пример 3. Найдем производную 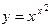 .
.
Здесь 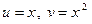 .
.
Значит,