Исследование функции
Функция 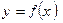 называется неубывающей (невозрастающей) на интервале
называется неубывающей (невозрастающей) на интервале 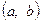 , если для всех
, если для всех 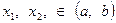 , таких, что
, таких, что 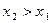 , выполняется:
, выполняется: 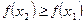
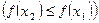 . Если в последних неравенствах стоит знак строгого неравенства,
. Если в последних неравенствах стоит знак строгого неравенства,
т. е. > (<), то функция называется возрастающей (убывающей):
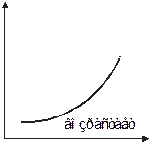 | 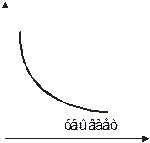 |
Признак монотонности функции. Если функция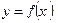 дифференцируема на интервале
дифференцируема на интервале 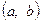 и
и 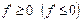 на
на 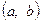 , то функция
, то функция 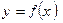 не убывает (не возрастает) на
не убывает (не возрастает) на 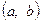 . Если в последних неравенствах стоит знак строгого неравенства, т. е. > (<), то функция возрастает (убывает) на
. Если в последних неравенствах стоит знак строгого неравенства, т. е. > (<), то функция возрастает (убывает) на 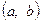 .
.
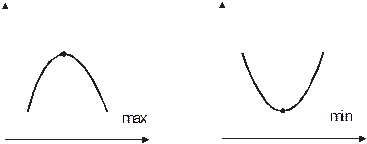
Точка 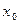 называется точкой локального максимума (минимума) функции
называется точкой локального максимума (минимума) функции 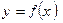 , если для всех
, если для всех 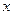 из некоторой окрестности точки
из некоторой окрестности точки 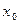 выполняется неравенство:
выполняется неравенство: 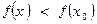
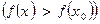 при
при 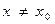 . Локальный минимум (min) и локальный максимум (max) называются локальным экстремумом.
. Локальный минимум (min) и локальный максимум (max) называются локальным экстремумом.
 |
Необходимое условие локального экстремума. Если
функция 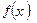 имеет в точке
имеет в точке 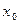 локальный экстремум и, дифференцируема в этой точке, то
локальный экстремум и, дифференцируема в этой точке, то 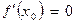 .
.
Точки, в которых 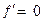 или производной не существует, называются точками возможного экстремума, или критическими точками. Точка возможного экстремума не обязательно всегда будет точкой экстремума. Для того, чтобы определить, будет ли точка
или производной не существует, называются точками возможного экстремума, или критическими точками. Точка возможного экстремума не обязательно всегда будет точкой экстремума. Для того, чтобы определить, будет ли точка 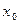 , в которой
, в которой 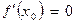 , точкой экстремума, необходимо воспользоваться достаточным условием локального экстрему-ма.Пусть функция
, точкой экстремума, необходимо воспользоваться достаточным условием локального экстрему-ма.Пусть функция  дифференцируема на отрезке
дифференцируема на отрезке 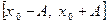 . Тогда, если
. Тогда, если 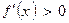
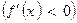 для всех
для всех 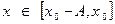 , а
, а 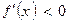
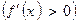 для всех
для всех 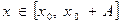 , то в точке
, то в точке 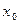 функция
функция 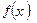 имеет локальный максимум (минимум); если же
имеет локальный максимум (минимум); если же 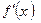 имеет на отрезке
имеет на отрезке 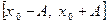 один и тот же знак, то в точке
один и тот же знак, то в точке 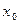 экстремума нет.
экстремума нет.
Другими словами, если 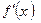 при переходе через точку
при переходе через точку 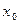 меняет знак с «+» на «—», то
меняет знак с «+» на «—», то 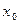 — точка локального максимума; если
— точка локального максимума; если 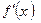 в точке
в точке 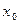 меняет знак с «—» на «+», то
меняет знак с «—» на «+», то 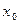 — точка локального минимума.
— точка локального минимума.
Второй достаточный признак существования экстремума. Если в критической точке вторая производная функции отрицательна, то функция в этой точке имеет максимум. Если вторая производная положительна, — минимум.
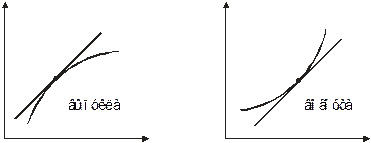
Говорят, что функция 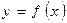 имеет выпуклость вверх (выпуклость), если график этой функции на
имеет выпуклость вверх (выпуклость), если график этой функции на 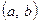 расположен ниже любой касательной к графику функции на
расположен ниже любой касательной к графику функции на 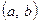 . Функция выпукла вниз (вогнута) на
. Функция выпукла вниз (вогнута) на 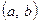 , если график этой функции расположен выше касательной на
, если график этой функции расположен выше касательной на 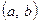 .
.
 |
Если функция 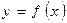 имеет на интервале
имеет на интервале 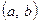 вторую производную и
вторую производную и 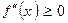
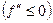 во всех точках
во всех точках 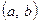 , то функция
, то функция 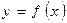 имеет на
имеет на 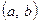 вогнутость (выпуклость).
вогнутость (выпуклость).
Точка перегиба функции — это точка, в которой направление выпуклости меняется на обратное. Например, функция 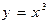 имеет точку перегиба
имеет точку перегиба 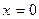 :
:
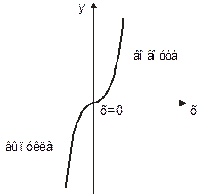 |
Необходимое условие точки перегиба. Если функция 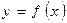 имеет перегиб в точке
имеет перегиб в точке 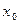 и существует вторая производная в этой точке, тогда
и существует вторая производная в этой точке, тогда 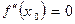 .
.
Достаточное условие точки перегиба. Пусть функция 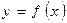 имеет вторую производную в некоторой окрестности точки
имеет вторую производную в некоторой окрестности точки 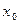 . Тогда, если в пределах этой окрестности
. Тогда, если в пределах этой окрестности 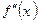 имеет разные знаки слева и справа от точки
имеет разные знаки слева и справа от точки 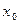 , функция
, функция 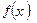 имеет перегиб в точке
имеет перегиб в точке 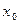 .
.
Прямая 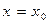 называется вертикальной асимптотой функции
называется вертикальной асимптотой функции 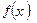 , если хотя бы одно из предельных значений
, если хотя бы одно из предельных значений 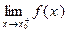 или
или 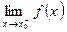 равно
равно 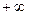 , или
, или 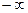 . Запись
. Запись 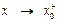 означает, что
означает, что 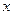 стремится к
стремится к 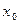 справа, соответственно,
справа, соответственно, 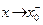 — слева.
— слева.
Например 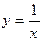 имеет вертикальную асимптоту
имеет вертикальную асимптоту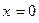 ,
,
т. к. 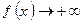 при
при 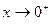 и
и 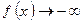 при
при 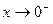 .
.
Прямая, 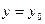 называется горизонтальной асимптотой функции
называется горизонтальной асимптотой функции 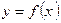 при
при 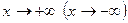 , если
, если 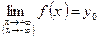 .
.
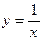 | 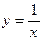 |
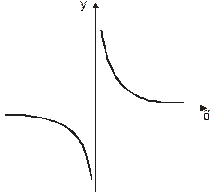 Например, функция
Например, функция 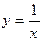 имеет горизонтальную асимптоту
имеет горизонтальную асимптоту 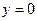 при
при 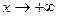 и при
и при 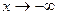 .
.
Прямая 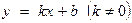 называется наклонной асимптотой функции
называется наклонной асимптотой функции 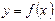 при
при 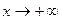
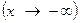 , если
, если 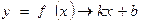 при
при 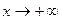
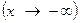 .
.
Наклонную асимптота находится из следующих соотношений:
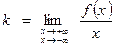 ;
; 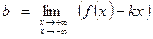 (9.1)
(9.1)
Полное исследование функции проводится на основе следующего плана:
1. Найти область определения функции 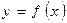 .
.
2. Исследовать функцию на периодичность. Если функция периодична, то необходимо найти основной период Т, с тем, чтобы, исследовав функцию и построив ветвь графика на промежутке 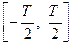 , построить затем, воспользовавшись периодичностью, весь график.
, построить затем, воспользовавшись периодичностью, весь график.
3. Найти точки х, в которых 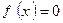 (это будут точки пересечения графика с осью
(это будут точки пересечения графика с осью 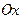 ), а также у , такие, что
), а также у , такие, что 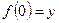 .
.
4. Отметить на оси 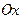 точки, найденные в пункте 3, и точки, в которых функция не определена, найденные в пункте 1. Эти точки разбивают ось
точки, найденные в пункте 3, и точки, в которых функция не определена, найденные в пункте 1. Эти точки разбивают ось 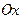 на несколько промежутков, на каждом из которых функция сохраняет постоянный знак. Установить знак функции на каждом из промежутков.
на несколько промежутков, на каждом из которых функция сохраняет постоянный знак. Установить знак функции на каждом из промежутков.
5. Исследовать функцию на четность и нечетность.
В случае четности или нечетности функции можно ограничиться исследованием и построением графика при 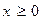 , а затем воспользоваться симметрией графика: график четной функции симметричен относительно оси
, а затем воспользоваться симметрией графика: график четной функции симметричен относительно оси 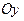 ; график нечетной функции симметричен относительно начала координат.
; график нечетной функции симметричен относительно начала координат.
6. Найти вертикальные, горизонтальные и наклонные асимптоты.
7. Определить участки возрастания и убывания функции. Найти экстремумы.
8. Определить участки выпуклости, вогнутости. Определить точки перегиба.
9. Получить несколько контрольных значений и построить график.
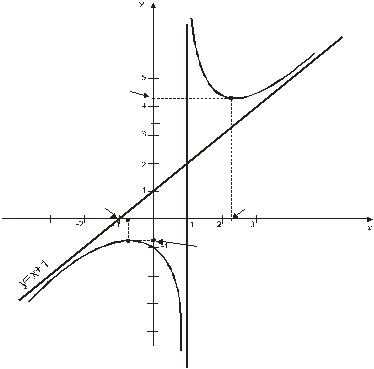
Пример. Исследовать и построить график функции 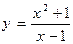 .
.
1. Областью определения функции являются все точки прямой 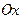 , за исключением точки
, за исключением точки 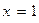 , т. к. в этой точке функция не определена (знаменатель обращается в нуль).
, т. к. в этой точке функция не определена (знаменатель обращается в нуль). 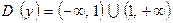 .
.
2. Функция не является периодичной.
3. Найдем точки пересечения с осями координат. С осью  :
:
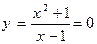 .
.
Так как 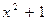 не имеет вещественных корней, то функция не имеет точек пересечения с
не имеет вещественных корней, то функция не имеет точек пересечения с 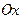 . С осью
. С осью 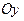 :
: 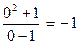 . Функция пересекает
. Функция пересекает 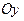 в точке
в точке 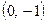 .
.
 4. Точка
4. Точка 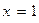 разбивает ось
разбивает ось  на два промежутка. На промежутке
на два промежутка. На промежутке 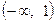 функция отрицательна, на
функция отрицательна, на 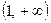 — функция положительна, так как, если подставить точки
— функция положительна, так как, если подставить точки 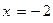 и
и 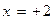 в уравнение функции, то получим:
в уравнение функции, то получим:
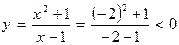 .
.
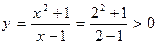 .
.
5. Исследуем на четность и нечетность: 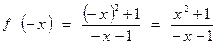 . Функция не является ни четной, ни нечетной.
. Функция не является ни четной, ни нечетной.
6. Найдем асимптоты функции. Вначале пытаемся найти вертикальную асимптоту. Исследуем поведение функции вблизи точки разрыва 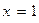 . Так как
. Так как 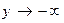 при
при 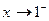 ,
, 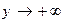 при
при 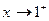 , то прямая
, то прямая 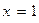 является вертикальной асимптотой функции. Если
является вертикальной асимптотой функции. Если 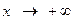 (
(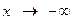 ), то
), то 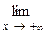
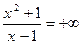 ,
, 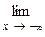
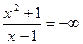 . Следовательно, горизонтальной асимптоты нет.
. Следовательно, горизонтальной асимптоты нет.
Выясним, имеется ли наклонная асимптота. Если существуют конcтанты 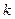 и b
и b 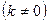 , определяемые соотношениям (9.1), то наклонная асимптота существует:
, определяемые соотношениям (9.1), то наклонная асимптота существует:
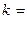
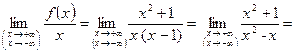
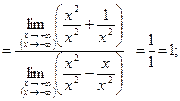
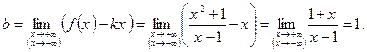
Следовательно, при 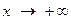 и при
и при 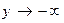 функция имеет наклонную асимптоту
функция имеет наклонную асимптоту 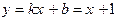 .
.

7. Для определения критических точек функции необходимо найти первую производную функции и приравнять ее к нулю:
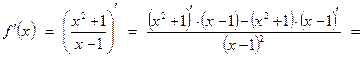
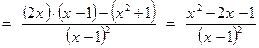 .
.
 . Значит
. Значит 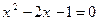 . Решая это квадратное уравнение, получаем:
. Решая это квадратное уравнение, получаем:
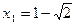 ;
; 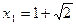 .
.
Находим интервалы знакоопределенности производной 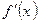 .
.
 |
Для этого необходимо подставить произвольные точки из промежутков. 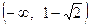 ,
, 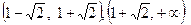 . Например, для определения знака производной на промежутке
. Например, для определения знака производной на промежутке 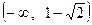 подставим
подставим 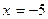 в уравнение для
в уравнение для 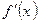 . Получим:
. Получим:
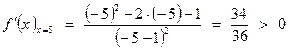 .
.
Следовательно, получим, что функция на 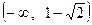 возрастает, на
возрастает, на 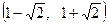 убывает, на
убывает, на 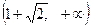 возрастает. Точка
возрастает. Точка 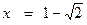 есть точка максимума, при этом:
есть точка максимума, при этом:
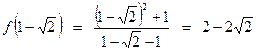 .
.
Точка 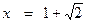 есть точка минимума, при этом
есть точка минимума, при этом 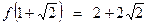 .
.
8. Определяем участки выпуклости, вогнутости и возможные точки перегиба. Для этого определим вторую производную:
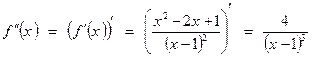 .
.
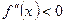 на
на 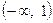 ;
; 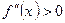 на
на 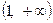 . Значит, на
. Значит, на 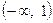 функция выпукла, а на
функция выпукла, а на 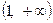 функция вогнута. Вторая производная
функция вогнута. Вторая производная 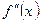 не обращается в нуль ни в какой точке, следовательно, точек перегиба нет.
не обращается в нуль ни в какой точке, следовательно, точек перегиба нет.
9. Построим график функции, используя все предыдущие пункты.

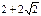 | |||||
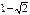 | |||||
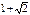 | |||||