Интегральное исчисление. Неопределенный интеграл
Функция 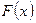 называется первообразной функции
называется первообразной функции 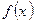 на некотором промежутке D, если для всех
на некотором промежутке D, если для всех 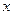 из D выполняется:
из D выполняется: 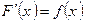 .
.
Например, 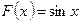 является первообразной для функции
является первообразной для функции 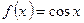 на всей числовой прямой, т. к.
на всей числовой прямой, т. к. 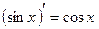 для всех
для всех 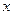 . Если
. Если 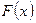 — первообразная для функции
— первообразная для функции 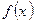 , то любая другая первообразная для
, то любая другая первообразная для 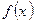 может быть представлена в виде
может быть представлена в виде 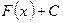 , где C — произвольная постоянная.
, где C — произвольная постоянная.
Неопределенным интегралом от функции 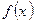 называется множество всех первообразных этой функции и обозначается
называется множество всех первообразных этой функции и обозначается 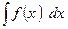 ; здесь
; здесь 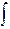 — знак интеграла,
— знак интеграла, 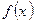 — подынтегральная функция,
— подынтегральная функция, 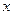 — переменная интегрирования.
— переменная интегрирования.
Согласно определению, 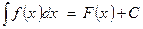 , где
, где 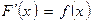 .
.
Введем объяснение записи 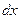 , которая обозначает дифференциал
, которая обозначает дифференциал 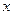 . Если функция
. Если функция 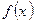 дифференцируема в точке х, то, значит, существует производная в этой точке, т. е.
дифференцируема в точке х, то, значит, существует производная в этой точке, т. е.
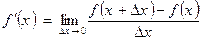 .
.
Согласно определению предела функции, можно записать, что:
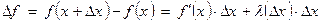 , где
, где 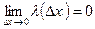 .
.
Дифференциалом функции 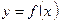 называется главная часть ее приращения, линейная относительно приращения аргумента, т. е. слагаемое
называется главная часть ее приращения, линейная относительно приращения аргумента, т. е. слагаемое 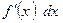 . Дифференциалом аргумента
. Дифференциалом аргумента 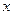 называется приращение аргумента:
называется приращение аргумента: 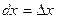 . Дифференциал функции
. Дифференциал функции 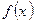 равен произведению ее производной на дифференциал аргумента:
равен произведению ее производной на дифференциал аргумента: 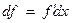
Следовательно, 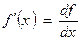 ;.
;.
Свойства дифференциала:
1. 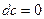 , где
, где  .
.
2. 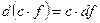 .
.
3. 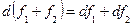 .
.
4. 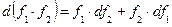 .
.
Запишем теперь свойства неопределенного интеграла.
1. 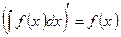 .
.
2. 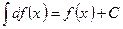 .
.
3. 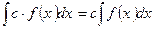 , где
, где  .
.
4. 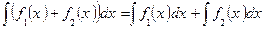 .
.
Отыскание неопределенного интеграла называется интегрированием функции.
Таблица основных интегралов:
1. 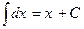 ;
;
2. 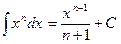 , при
, при 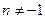 ;
;
3. 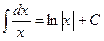 ;
;
4. 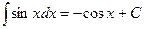 .
.
5. 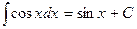 ;
;
6. 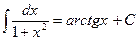 ;
;
7. 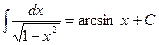 ;
;
8. 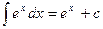 ;
;
9. 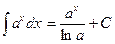 ;
;
10.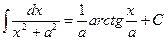 ;
;
11. 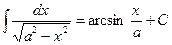 ;
;
12. 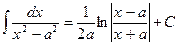 ;
;
13. 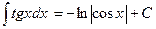 ;
;
14. 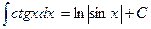 .
.
Интегралы иногда можно найти с помощью непосредственного использования таблицы интегралов и основных свойств неопределенного интеграла.
Пример 1. Найти: 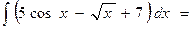
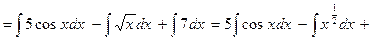
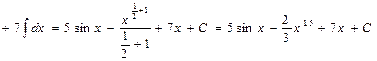 .
.
Во многих случаях интегралы можно найти путем введения новой переменной интегрирования. Этот метод называется методом подстановки, или методом замены переменной. Если 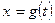 , тогда справедлива следующая формула замены переменной:
, тогда справедлива следующая формула замены переменной:
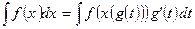 .
.
Пример 2. Найдем интеграл: 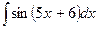 .
.
Необходимо ввести новую переменную t таким образом, чтобы свести данный интеграл к табличному. Обозначим
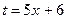 . Тогда
. Тогда 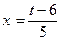 . Следовательно,
. Следовательно, 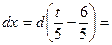
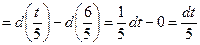 . Подставим найденные выражения в исходный интеграл:
. Подставим найденные выражения в исходный интеграл: 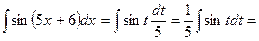
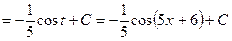 .
.
Пример 3. Найдем интеграл: 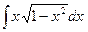 .
.
Введем переменную 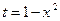 . Тогда
. Тогда 
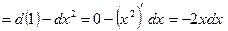 .
.
Следовательно, 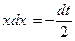 . Подставим найденные выражения в интеграл:
. Подставим найденные выражения в интеграл: 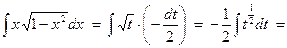
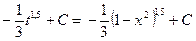 .
.
Существует еще один метод интегрирования: интегрирование по частям. Если функции  и
и 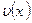 определены и дифференцируемы на некотором множестве D, тогда справедлива формула интегрирования по частям:
определены и дифференцируемы на некотором множестве D, тогда справедлива формула интегрирования по частям:
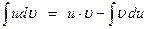 .
.
Эта формула позволяет свести вычисление 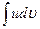 к вычислению
к вычислению 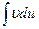 , который иногда может оказаться более простым.
, который иногда может оказаться более простым.
Пример 4. Найдем 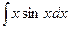 .
.
Обозначим 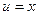 ;
; 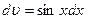 .
.
Для того, чтобы воспользоваться формулой интегрирования по частям, необходимо найти 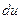 и
и 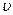 .
.
Найдем: 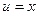 . Значит
. Значит 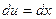 .
.
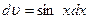 . Значит:
. Значит: 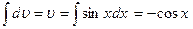 .
.
Подставим найденные значения в формулу интегрирования по частям:
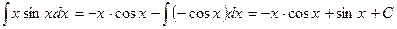 .
.
Пример 5. Найдем: 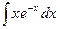 .
.
Обозначим: 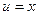 ,
, 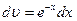 .
.
Тогда 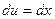 . Найдем
. Найдем 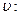
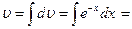
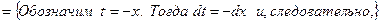
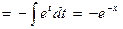 .
.
Таким образом, 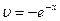 . Поставим найденные выражения в формулу интегрирования по частям:
. Поставим найденные выражения в формулу интегрирования по частям:
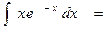
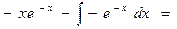
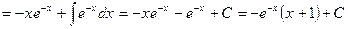 .
.