Определенный интеграл

Площадь криволинейной трапеции АВСD, ограниченной линиями 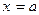, , 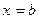, 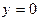находится как: 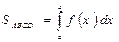, где — определенный интеграл, a и b есть границы интегрирования.

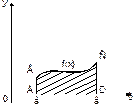
Определенный интеграл находят с помощью формулы Ньютона—Лейбница:

 

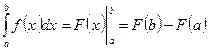, где 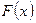есть первооб-разная .

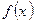Свойства определенного интеграла:

1. .

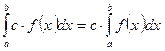2. .

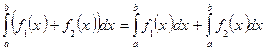3. 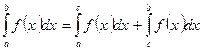, где .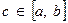

Пример 1. 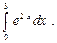Введем новую переменную: t=2x. Тогда 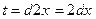. Следовательно, 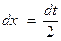. Найдем пределы интегрирования для переменной t, т. к. 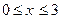, следовательно, 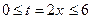. Таким образом:

.

 

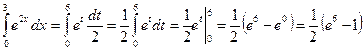Рассмотрим фигуру, представляющую собой множество то-

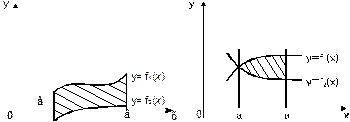чек, ограниченных линиями: x=a, x=b. , , .

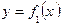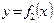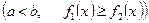Тогда площадь заштрихованной фигуры вычисляется по формуле:

 

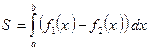(11.1)

Пример 2. Вычислим площадь фигуры, ограниченной линиями: .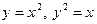

 

Вначале схематически построим графики указанных линий.

 

 

 

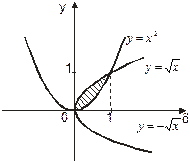
Для этого необходимо решить систему уравнений:

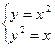
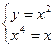
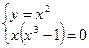
Из последнего уравнения находим абсциссы точек пересечения:

 

Найдем указанную площадь, воспользовавшись формулой (11.1).

 

.

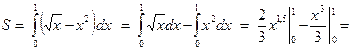
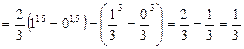Пример 3. Вычислить площадь фигуры, ограниченной линиями: , .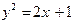

 

 

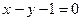Построим схематически графики указанных линий.

 

 

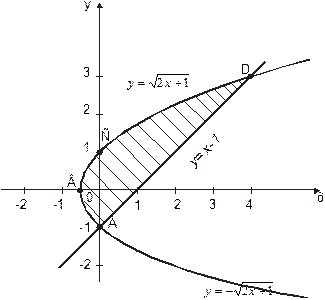Нам необходимо найти площадь заштрихованной фигуры. Найдем точки пересечения этих линий. Решим систему:

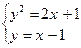
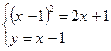
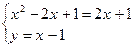
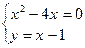
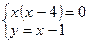
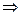
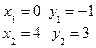
Указанную площадь можно искать двумя способами.