Метод Гаусса решения СЛАУ
Приведем использование метода Гаусса для решения СЛАУ, состоящей из трех уравнений с тремя неизвестными:

Вначале составляем расширенную матрицу:
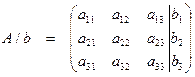
Затем эту матрицу приводят к ступенчатому виду, в котором все элементы, стоящие ниже главной диагонали матрицы А, равны нулю, т. е.:

Для получения ступенчатого вида можно менять местами строки матрицы, умножать все элементы строки на одно число, прибавлять к строке другую строку, умноженную на некоторое число. Тогда из последнего уравнения следует, что:
 .
.
Следовательно: 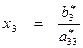 .
.
Найденное значение 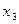 подставляем в предпоследнее уравнение, откуда находим
подставляем в предпоследнее уравнение, откуда находим  :
:
 .
.
Значит:  .
.
Затем найденные значения  и
и 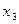 подставляем в первое уравнение и находим
подставляем в первое уравнение и находим 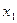 .
.
Пример. Решить СЛАУ методом Гаусса.

Расширенная матрица системы будет иметь вид:

Вычитаем из второй строки первую, умноженную на 2. Затем из третьей строки вычитаем первую, умноженную на 3. Получаем:
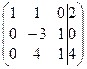
Теперь нужно получить во втором столбе на месте 4 число нуль. Чтобы не иметь дело с дробями, прибавим к третьей строке вторую и затем поменяем их местами. Получим:
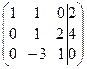
Теперь к третьей строке прибавим вторую, умноженную на 3. Получим:

Из последней строки получаем:  .
.
Значит:  .
.
Запишем уравнение, соответствующее второй строке матрицы:
 . Значит:
. Значит: 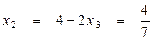 .
.
Подставляем  и
и 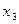 в первое уравнение и находим
в первое уравнение и находим 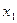 :
:
 ;
; 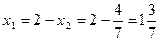 .
.
Метод Гаусса, в отличие от метода Крамера, пригоден и в тех случаях, когда 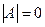 , т. е. когда система является неопределенной.
, т. е. когда система является неопределенной.
Пример.Решим СЛАУ:
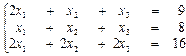
Запишем расширенную матрицу:
 ~
~ 
Здесь мы поменяли вначале местами первую и вторую строки, а затем из второй строки отняли первую, умноженную на 2, а из третьей отняли первую, умноженную на 2. Получили нулевую строку, т. е. для двух уравнений получили три неизвестных. В таких случаях система имеет бесконечное множество решений.
Решение записывают в следующем виде. Одну из переменных, например, 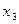 , обозначают за константу с, а остальные переменные выражают из не нулевых строк с учетом этой константы. Например:
, обозначают за константу с, а остальные переменные выражают из не нулевых строк с учетом этой константы. Например:  . Из второго уравнения получаем:
. Из второго уравнения получаем: 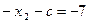 . Значит:
. Значит: 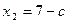 .
.
Из первого уравнения:  .
.
Следовательно, получаем общее решение:

Придавая с конкретные значения, мы можем получить частные решения. Например, при получаем:
получаем:

При 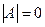 система может быть несовместной. Рассмотрим такой пример:
система может быть несовместной. Рассмотрим такой пример:

Запишем расширенную матрицу и приведем ее к ступенчатому виду:
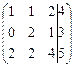 ~
~ 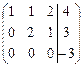
Из третьей строки следует, что третье уравнение будет иметь вид:  .
.
Получили противоречивую запись; следовательно, данная система не имеет решений.