Теоретические упражнения
1. Доказать, что функция 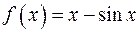 монотонно возрастает на отрезке: а)
монотонно возрастает на отрезке: а)  ; б)
; б) 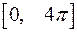 Следует ли из монотонности дифференцируемой функции монотонность ее производной?
Следует ли из монотонности дифференцируемой функции монотонность ее производной?
2. Доказать теорему: если функции  и
и 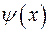 дифференцируемы на отрезке
дифференцируемы на отрезке 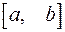 и
и 
 , а
, а 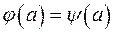 , то
, то 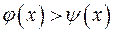
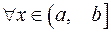 .
.
Дать геометрическую интерпретацию теоремы.
У к а з а н и е. При доказательстве теоремы установить и использовать монотонность функции  .
.
3. Доказать неравенство  для трех случаев:
для трех случаев:
а) 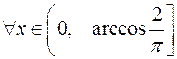 ;
;
б) 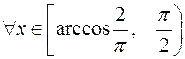 ;
;
в) 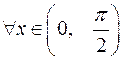 .
.
Дать геометрическую интерпретацию неравенства.
4. Исходя из определений минимума и максимума, доказать, что функция
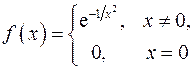
имеет в точке 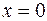 минимум, а функция
минимум, а функция
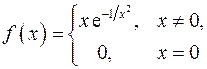
не имеет в точке 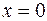 экстремума.
экстремума.
5. Исследовать на экстремум в точке  функцию
функцию 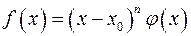 , считая, что производная
, считая, что производная  не существует, но функция
не существует, но функция  непрерывна в точке
непрерывна в точке  и
и 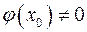 ,
,  .— натуральное число.
.— натуральное число.
6. Исследовать знаки максимума и минимума функции 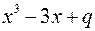 и выяснить условия, при которых уравнение
и выяснить условия, при которых уравнение  имеет а) три различных действительных корня; б) один действительный корень.
имеет а) три различных действительных корня; б) один действительный корень.
7. Определить «отклонение от нуля» многочлена  на отрезке
на отрезке 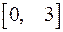 , т. е. найти на этом отрезке наибольшее значение функции
, т. е. найти на этом отрезке наибольшее значение функции  .
.
8. Установить условия существования асимптот у графика рациональной функции.