Численные методы.
Значения элементарных функций и многочисленных специальных математических функций в вещественных и комплексных точках с вещественными координатами, можно найти, просто вычислив соответствующие выражения. Найдем, например, значение функции синус в точке 0.7 и значение функции Бесселя 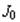 (x) первого рода нулевого порядка в комплексной точке 1.+0.5I:
(x) первого рода нулевого порядка в комплексной точке 1.+0.5I:
Sin[0.7]
BesselJ[0, 1. + 0.5 I]
Команды символьных вычислений Sum,Integrate, DSolve и т.п. имеют своих двойников NSum, NIntegrate, NDSolve и т.д., выполняющих приближенные численные вычисления.
Integrate[Sin[x^4 + x], {x, 1, 2}]
Вычисления не произошло, так как не удалось символьно вычислить соответствующий неопределенный интеграл. Однако определенный интеграл можно вычислить приближенно с любой степенью точности
NIntegrate[Sin[x^4 + x], {x, 1, 2}, WorkingPrecision -> 25]
Приближение дискретных данных с наименьшим среднеквадратичным отклонением с помощью задаваемой пользователем системы функций осуществляет команда Fit. В рассмотренном ниже примере порождается 10 случайных точек на координатной плоскости и находятся наилучшие приближения с помощью полинома третьей степени или показательных функций 1, E^x, E^(2x), E^(3x)
data = Table[{Random[], Random[]}, {i, 10}] poly = Fit[data, {1, x, x^2, x^3}, x] expo = Fit[data, {1, E^x, E^(2x), E^(3x)}, x]
С помощью команды FindMinimum можно численно найти минимум функции на заданном множестве. Найдем, например, первый минимум функции Бесселя BesselJ[0,x] на отрезке [0,5]. Прежде всего, найдем грубо положение минимума, нарисовав график функции
Plot[BesselJ[0, x], {x, 0, 5}];
Мы видим, что минимум расположен вблизи точки x = 4. Уточним его положение
FindMinimum[BesselJ[0, x], {x, 4}]
ФункцияConstrainedMin находит минимум линейной функции от нескольких аргументов в области, ограниченной системой линейных неравенств
ConstrainedMin[2x - 3y, {x > y, y > 1, 2x + y < 5}, {x, y}]
Численное решение дифференциальных уравнений как обыкновенных, так и в частных производных можно осуществлять командой NDSolve. Найдем, например, численно решение задачи Коши для системы уравнений Лоренца и нарисуем фазовый портрет решения
slv = NDSolve[{x'[t] == -3(x[t] - y[t]), y'[t] == -x[t]z[t] + 30x[t] - y[t], z'[t] == x[t]y[t] - z[t], x[0] == 0, y[0] == 1, z[0] == 0}, {x[t], y[t], z[t]}, {t, 0, 30}, MaxSteps -> 10000, Method -> RungeKutta, MaxStepSize -> 0.004]; ParametricPlot3D[Evaluate[{x[t], y[t], z[t]} /. slv], {t, 0, 30}];
Фазовый портрет иллюстрирует наличие так называемого "странного аттрактора" у траекторий системы Лоренца [13].
2. Разработка заданий для выполнения лабораторных и расчётно-графических работ по курсу «Вычислительная математика»
2.1. Лабораторная работа №1.
Знакомство с пакетом MathCAD 2000
2.1.1. Простейшие приёмы работы.