Порядок выполнения лабораторной работы с помощью метода простых итераций.

Графически или аналитически отделить корень уравнения f(x) = 0.

1. Преобразовать уравнение f(x) = 0 к виду x = j(x) так, чтобы в некоторой окрестности [a,b] корня x производная j¢(x) удовлетворяла условию |j¢(x)|£q<1. При этом следует помнить, что чем меньше q, тем быстрее последовательные приближения сходятся к корню.

2. Выбрать начальное приближение, лежащее на отрезке [a,b].

3. Используя пакет MathCAD, написать функцию для нахождения корня уравнения.

4. Провести вычисления для заданной функции.

 

2.3.3. Приближённое решение уравнения методом Ньютона.

Если известно хорошее начальное приближение решения уравнения f(x) = 0, то эффективным методом повышения точности является метод Ньютона (метод касательных). Метод состоит в построении итерационной последовательности x_n+1 = x_n – f(x_n)/f¢(x_n), сходящейся к корню уравнения f(x) = 0. Сформулируем достаточные условия сходимости метода [10].

Теорема. Пусть f(x) определена и дважды дифференцируема на [a,b], причём f(a)f(b)<0, а производные f¢(x), f²(x) сохраняют знак на отрезке [a,b]. Тогда, исходя из начального приближения x₀Î[a,b], удовлетворяющего неравенству f¢(x₀)f²(x₀)>0, можно построить последовательность

, n = 0,1,2,…,

сходящуюся к единственному на [a,b] решению x уравнения f(x) = 0.

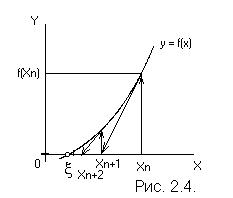
Метод Ньютона допускает простую геометрическую интерпретацию. Если через точку с координатами (x_n;f(x_n)) (рис. 2.4) провести касательную, то абсцисса точки пересечения этой касательной с осью Ox и есть очередное приближение x_n+1 корня уравнения f(x) = 0.

Для оценки погрешности n-го приближения корня можно воспользоваться неравенством

,

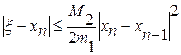где M₂ – наибольшее значение модуля второй производной |f²(x)| на отрезке [a,b]; m₁ –наименьшее значение модуля первой производной |f¢(x)| на отрезке [a,b]. Таким образом, если |x_n – x_n-1|<e, то |x - x_n|£M₂e²/(2m₁). Последнее соотношение означает, что при хорошем начальном приближении корня после каждой итерации число верных десятичных знаков в очередном приближении удваивается, т.е. процесс сходится очень быстро. Значит, если необходимо найти корень с точностью e, то итерационный процесс можно прекратить, когда

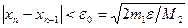
Опишем один шаг итераций. Если на (n – 1)-м шаге очередное приближение x_n-1 не удовлетворяет условию окончанию процесса, то вычисляем величины f(x_n-1), f¢(x_n-1) и следующее приближение корня x_n = x_n-1 – f(x_n-1)/f¢(x_n-1). При выполнении условия

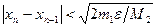
величину x_n принимаем за приближённое значение корня x, вычисленное с точностью e [10].

Метод Ньютона эффективен, если известно хорошее начальное приближение для корня и в окрестности корня график функции имеет большую крутизну. В этом случае процесс быстро сходится [10].