Метод Чебышева.

Требуется найти вещественный корень уравнения f(x) = 0, изолированный в интервале (a, b). Функция f(x) предполагается непрерывной вместе с производными до n-го порядка включительно, причём в интервале (a, b) 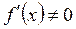[5]. Рассмотрим кривую 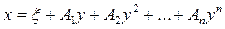. Распорядимся параметрами ξ, A₁, A₂, …, A_n так, чтобы кривые y=f(x) и 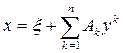в точке с абсциссой x₀ из интервала (a, b) имели касание n-го порядка. Говорят, что кривые y=f(x) и y=φ(x) в точке с абсциссой x₀ имеют касание n-го порядка, если

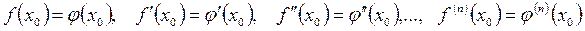
Геометрически точка касания n-го порядка является предельным положением (n+1) точек пересечения кривых y=f(x) и y=φ(x) при стремлении этих точек пересечения к точке с абсциссой x₀. В данном случае кривая y=φ(x) неявно определяется уравнением 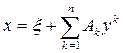[5].

При таком выборе параметров ξ, A₁, A₂, …, A_n за приближённое значение искомого корня можно принять абсциссу точки пересечения кривой 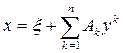с осью Ox, т.е. число ξ.

Если n=1, то (способ Ньютона).

Если n=2, то 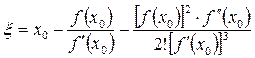. (2.15)

Если n=3, то 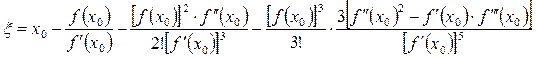(2.16)

Если n=4, то

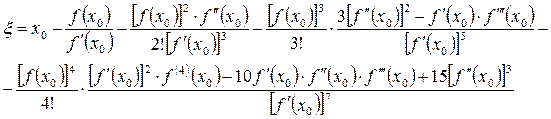(2.17)

Приведём оценки погрешности значений корней, найденных по формулам (2.15) и (2.16).

Для формулы (2.15) при n=2

.

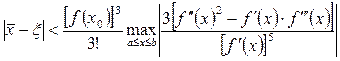Для формулы (2.16) при n=3

.
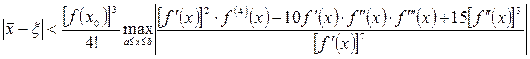