Метод простых итераций.

Рассмотрим произвольную нелинейную систему уравнений в Rⁿ [10].

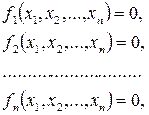
или в более краткой векторной форме

f(x) = 0,

здесь .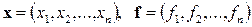

Метод простых итераций (метод последовательных приближений) решения системы состоит в замене исходной системы эквивалентной ей системой

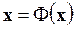
и построении последовательности

,

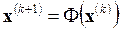сходящейся при 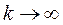к исходному решению 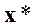системы. Таким образом, данный метод является естественным обобщением метода простых итераций для одного уравнения [10].

Близость последовательных приближений (итераций) 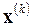к точному решению x определяется по-разному для разных норм вектора. Нетрудно показать, что

,

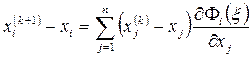где ξ – точка, лежащая между точками n-мерного пространства 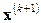и x на прямой, соединяющей эти точки.

Из этого равенства видно, что сходимость итераций определяется свойствами матрицы производных 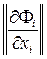и имеет место, если какая-либо её норма, согласованная с нормой вектора, меньше единицы.

На практике рассматривают матрицу

.

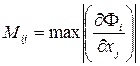Норма этой матрицы мажорирует соответствующие нормы матрицы производных. Поэтому достаточным условием сходимости является условие .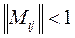

Для различных норм матрицы это условие принимает разные формы:

.

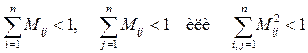Поскольку в конечномерном пространстве все нормы матриц эквивалентны, из сходимости итераций в одной норме следует сходимость во всех остальных.

Нулевое приближение в случае n = 2 можно выбрать графически, изобразив в плоскости (x₁, x₂) кривые 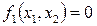и 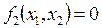и определив приближённо точки их пересечения.

Итерации можно заканчивать, когда

.

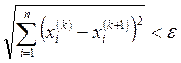За приближённое значение решения принимаем .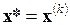

Если нарушается условие монотонного убывания величины

,

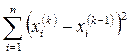то можно считать условие сходимости нарушенным [10].