Метод наискорейшего спуска.
Общий недостаток всех рассмотренных выше методов решения систем нелинейных уравнений – это сугубо локальный характер сходимости, затрудняющий их применение в случаях, когда имеются проблемы с выбором хороших начальных приближений. Чтобы решить такую задачу, нужно поставить задачу нахождения решений данной нелинейной системы как оптимизационную или, иначе, экстремальную задачу [1].
Из функций f и g системы 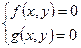 образуем новую функцию
образуем новую функцию
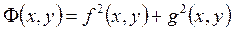 . (2.22)
. (2.22)
Так как эта функция неотрицательна, то найдётся точка (и не единственная) 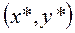 такая, что
такая, что
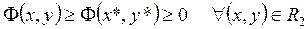 ,
,
т.е. 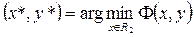 . Следовательно, если тем или иным способом удаётся получить точку
. Следовательно, если тем или иным способом удаётся получить точку 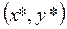 , минимизирующую функцию
, минимизирующую функцию 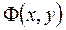 , и если при этом окажется, что
, и если при этом окажется, что 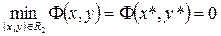 , то
, то 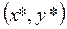 - искомое решение системы
- искомое решение системы 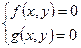 , поскольку
, поскольку
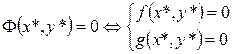 .
.
Последовательность точек 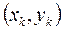 - приближёний к точке
- приближёний к точке 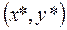 минимума
минимума 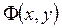 - обычно получают по рекуррентной формуле
- обычно получают по рекуррентной формуле
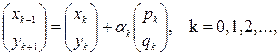 (2.23)
(2.23)
где 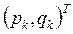 - вектор, определяющий направление минимизации, а
- вектор, определяющий направление минимизации, а 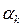 - скалярная величина, характеризующая величину шага минимизации (шаговый множитель). Учитывая геометрический смысл задачи минимизации функции двух переменных
- скалярная величина, характеризующая величину шага минимизации (шаговый множитель). Учитывая геометрический смысл задачи минимизации функции двух переменных 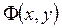 - «спуск на дно» поверхности z =
- «спуск на дно» поверхности z = 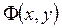 (см. лаб. раб. №7), итерационный метод (2.23) можно назвать методом спуска, если вектор
(см. лаб. раб. №7), итерационный метод (2.23) можно назвать методом спуска, если вектор 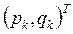 при каждом k является направлением спуска (т.е. существует такое α > 0, что
при каждом k является направлением спуска (т.е. существует такое α > 0, что 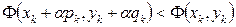 ) и если множитель
) и если множитель 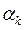 подбирается так, чтобы выполнялось условие релаксации
подбирается так, чтобы выполнялось условие релаксации 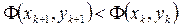 , означающее переход на каждой итерации в точку с меньшим значением минимизируемой функции.
, означающее переход на каждой итерации в точку с меньшим значением минимизируемой функции.
Итак, при построении численного метода вида (2.23) минимизации функции 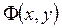 следует ответить на два главных вопроса: как выбирать направление спуска
следует ответить на два главных вопроса: как выбирать направление спуска 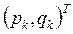 и как регулировать длину шага в выбранном направлении с помощью скалярного параметра – шагового множителя
и как регулировать длину шага в выбранном направлении с помощью скалярного параметра – шагового множителя 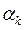 .
.
При выборе направления спуска естественным является выбор такого направления, в котором минимизируемая функция убывает наиболее быстро. Как известно из математического анализа функции нескольких переменных, направление наибольшего возрастания функции в данной точке показывает её градиент в этой точке. Поэтому примем за направление спуска вектор
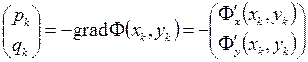
- антиградиент функции 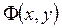 . Таким образом, из семейства методов (2.23) выделяем градиентный метод
. Таким образом, из семейства методов (2.23) выделяем градиентный метод
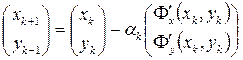 . (2.24)
. (2.24)
Оптимальный шаг в направлении антиградиента – это такой шаг, при котором значение 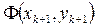 - наименьшее среди всех других значений
- наименьшее среди всех других значений 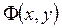 в этом фиксированном направлении, т.е. когда точка
в этом фиксированном направлении, т.е. когда точка 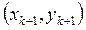 является точкой условного минимума. Следовательно, можно рассчитывать на наиболее быструю сходимость метода (2.24), если полагать в нём
является точкой условного минимума. Следовательно, можно рассчитывать на наиболее быструю сходимость метода (2.24), если полагать в нём
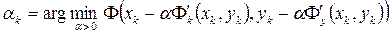 . (2.25)
. (2.25)
Такой выбор шагового множителя, называемый исчерпывающим спуском, вместе с формулой (2.24) определяет метод наискорейшего спуска [1].