Аппроксимация с помощью кубического сплайна.

Специальным видом кусочной интерполяции является интерполяция с помощью сплайн-функции. Образованные в процессе такой интерполяции кривые обладают достаточным приближением и образуют кусочно-кубический полином. Сплайн-интерполяция по сравнению с другими методами интерполяции обеспечивает наилучшее приближение. Ниже исследуется сплайн-интерполяция с помощью кубических полиномов [10].

Пусть имеется некоторая кривая f(x), а для неё известен набор опорных точек x_i, y_i (i=0..n), где n - количество интервалов между ними. На каждом интервале исходная функция аппроксимируется кубическим полиномом (сплайном)

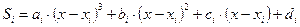(2.26)

Для n интервалов необходимо найти 4*n неизвестных, поскольку для каждого интерполирующего сплайна Sj вычисляются значения коэффициентов a_i, b_i, c_i, d_i.

Любой сплайн должен удовлетворять четырем условиям:

1. В каждой нижней границе интервала сплайн проходит через опорную точку.

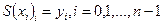(2.27)

2. В каждой верхней границе интервала сплайн проходит через опорную точку.

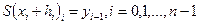(2.28)

Ширина интервала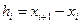

3. Для каждой нижней граничной точки интервала сплайн имеет одинаковую крутизну в обоих граничащих интервалах.

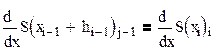
(2.29)

4. Для каждой верхней граничной точки интервала сплайн имеет одинаковую крутизну в обоих граничащих интервалах.

 

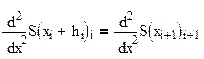
(2.30)

Для вычисления коэффициентов n интерполирующих сплайнов требуется ещё два условия. Эти условия назовём граничными и выберем произвольно:

а). через обе граничные точки кривая должна проходить с нулевой кривизной, превращаясь в прямую.

б) крутизна любого интерполирующего сплайна в обеих граничных точках фиксирована.

Вывод коэффициентов.

Вычислим 4*n коэффициентов с помощью заданных опорных точек. Проще всего определить коэффициенты а из первого условия.

Подставляя в (2.27) x = x_i, получаем

d_i = y_i, i = 0,1,…,n-1 (2.35)

Из второго условия подставляем уравнение (2.28) и x = x_i + h_i в (2.26) с учётом (2.35) получаем

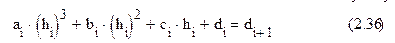
Согласно третьему условию:

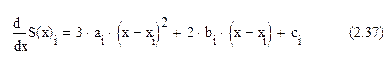
Подставляя в выражение (2.37) уравнение (2.29) имеем:

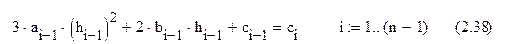
Для удовлетворения четвёртого условия вычислим вторую производную интерполирующего сплайна:

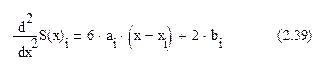
Подставляя в это выражение уравнение (2.30), получаем:

Посредством исключения коэффициентов а и с из уравнений (2.38), (2.36) и (2.40) вместе с граничными условиями (2.31), (2.32) или (2.33), (2.34) получаем систему линейных уравнений для всех b. Теперь решим (2.40) относительно

Подставив (2.41) в (2.36):

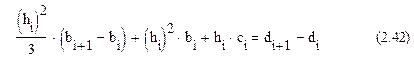
Это уравнение в свою очередь решим относительно

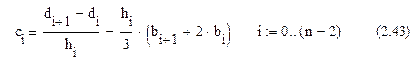
Для первого члена в правой части (2.43) в дальнейшем будем пользоваться сокращением

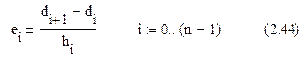
Опорные точки должны быть сопоставимы с непрерывной функцией, т.е. функция не должна иметь скачков, поскольку из-за h_i=0 значение e_i стремилось бы к бесконечности.

Чтобы исключить коэффициенты a_i, c_i подставим в уравнения (2.41) и (2.43) в уравнение (2.38) и после преобразования запишем:

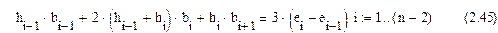
Оставшиеся два уравнения, необходимые для вычисления всех коэффициентов b_i получаем с помощью граничных условий. Таким образом задаются две системы уравнений.

Граничное условие А.

Подставляя уравнение (2.31) при i = 0 и x = x_i в уравнение (2.39), получаем

b₁ = 0 (2.46)

Для упрощённого расчёта граничного условия (2.32) допустим, что за опорной точкой x_n существует другой интерполирующий сплайн, для которого условия (2.27), (2.29) и (2.30) выполняются. Согласно последнему условию

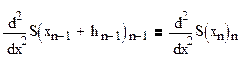
Подставляя это выражение при i = n и x = x_n в уравнение (2.39) получаем

b_n = 0 (2.47)

Аналогичным образом можно записать (2.45) и для i = n-1, т.е.:

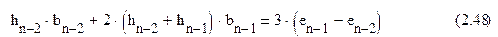
Уравнения (2.41) и (2.44) представляют собой систему линейных уравнений, с помощью которой вычисляется n-1 сплайн-коэффициентов b₁...b_n-1. В матрице коэффициентов заполненными оказываются только главная диагональ и две соседние диагонали, а все остальные элементы равны 0. Такая система уравнений называется трёхдиагональной.

После решения системы уравнений, приведённой выше, предполагается, что все коэффициенты b_i известны. С помощью уравнения (2.41) вычисляются все n a_i, а с помощью (2.43) - все коэффициенты c_i.

Граничное условие Б.

С учётом граничных условий (2.33) и (2.34) создаётся система из n уравнений для коэффициентов b_i. Подставляя (2.33) для i = 1 и x = x₁ получаем

c₁ = ma (2.50)

Из уравнения (2.43)

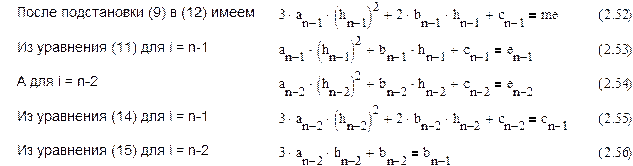
Таким образом, получаем систему уравнений

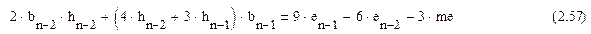
которую необходимо решить относительно b_n-1 и b_n-2

Уравнения (2.45), (2.51) и (2.57) образуют систему линейных уравнений всех сплайн-коэффициентов b₁...b_n-1. Сиcтема трёхдиагональна, однако её матрица коэффициентов в отличии от уравнения (2.49) не симметрична. После решения этой системы по уравнениям (2.53) и (2.41) рассчитаем коэффициенты a_i, а по уравнению (2.38) коэффициенты c_i.

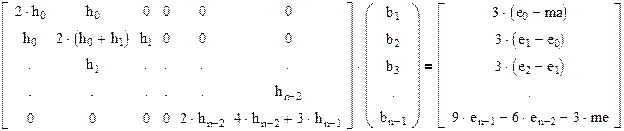
Моделирование сплайн-интерполяции.

Для исследования сплайн-интерполяции составим программу, вычисляющую сплайн-коэффициенты по граничному условию А.

Функция Spline реализует алгоритм вычисления сплайн-коэффициентов с учётом граничного условия А. Результатом вычисления является матрица размерностью n*4 в строках которой записаны коэффициенты a, b, c, d для каждой из n сплайн функции. Входные параметры - векторы x, y - исходные опорные точки.

Функция Function(x) вычисляет для заданного x значения сплайна.