Тригонометрическая интерполяция.

Пусть функция f(х) задана на отрезке [0,2p] таблицей значении f(x_i) в равноотстоящих узлах 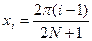(i=1, 2, ..., 2N+1). Тригонометрическим многочленом степени М называют многочлен [10]

.

Задача тригонометрической интерполяции состоит в построении тригонометрического интерполяционного многочлена наименьшей степени, удовлетворяющего условиям Pм(x_i)=f(x_i), i = l,…, 2N+1. Можно показать, что решением этой задачи является тригономет­рический многочлен

(2.58)

коэффициенты которого вычисляются по следующим формулам:

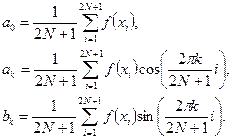(2.59)

Широкие возможности тригонометрической интерполяции сле­дуют из того факта, что с возрастанием N многочлен Р(х) аппроксимирует f(x) с возрастающей точностью, т. е.

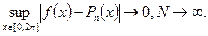
Это утверждение справедливо для достаточно широкого класса функций. Этим тригонометрическая интерполяция существенно отличается от алгебраической интерполяции на системе равноот­стоящих узлов. При алгебраическом интерполировании разность между функцией f(x) интерполяционным многочленом может быть как угодно большой всюду, кроме узлов интерполяции. Тригонометрическое интерполирование полностью свободно от этого недостатка [10].

Для вычисления коэффициентов (2.59) тригонометрического ин­терполяционного многочлена (2.58) предназначена подпрограмма Trigon(f, n, m):

где f – значение функции в узлах интерполяции;

n – количество равноотстоящих узлов x_i;

m – степень многочлена.