Метод градиентного спуска.

Общая задача нелинейного программирования без ограничений состоит в минимизации функции f(x)=f(x₁, x₂, ..., x_п}, заданной во всем n-мерном евклидовом пространстве. Функция f(х) называ­ется целевой функцией [10].

Как правило, численные методы отыскания экстремума состоят в построении последовательности векторов {х^(k)}, удо­влетворяющих условию f(х⁽⁰⁾)>f(х⁽¹⁾)>…>f(х⁽ⁿ⁾). Методы постро­ения таких последовательностей называются методами спуска. В этих методах элементы последовательности {х^(k)} вычисляются по формуле

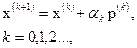(2.60)

где p^(k) – направление спуска; a_k – длина шага в этом направлении.

Как известно, градиент функции в некоторой точке х^(k) направлен в сторону наискорейшего локального возрастания функции. Следовательно, спускаться нужно в направлении, про­тивоположном градиенту. Вектор, противоположный градиенту, называется антиградиентом. Выбирая антиградиент в качестве направления спуска, приходят к итерационному процессу вида

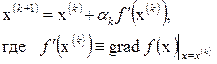(2.61)

Все методы спуска, в которых вектор р^(k) совпадает с антиградиентом, называются градиентными методами. Они от­личаются друг от друга только способом выбора шага. Наиболее употребительны метод наискорейшего спуска и метод дробления шага. В методе наискорейшего спуска величина a_k определяется из условия

,

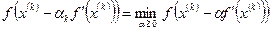т. е. на каждом шаге решается од­номерная задача минимизации. Гео­метрическая интерпретация этого ме­тода достаточно проста (рис. 2.7). Заметим, что на двух последова­тельных шагах направления спуска ортогональны [10].

Рис. 2.7.

Если f(х) – ограниченная снизу не­прерывно дифференцируемая функция и для некоторой начальной точки х⁽⁰⁾ множество {х:f(х)<f(х⁽⁰⁾)} также огра­ничено, то для метода наискорейшего спуска последовательность {х^(k)} либо сходится к точке минимума при k®¥, либо достигает точки минимума за конечное число шагов.

В данной лабораторной работе для минимизации функции использован метод градиентного спуска с дроблением шага. Процесс (2.61) с дроблением шага протекает следующим образом. Выбираем некоторое начальное значение х⁽⁰⁾. Общих правил выбора х⁽⁰⁾ нет; если есть информация об области расположения искомой точки минимума, то точку х⁽⁰⁾ выбираем в этой области. Затем выбираем некоторое a_k = a = const и на каждом шаге процесса (2.61) проверяем условие монотонности f(х^(k+1)) <f(х^(k)). Если это условие нарушается, то a дробим до тех пор, пока монотонность не восстановится. Для окончания счета можно использовать различные критерии. В данной работе итерации прекращаем, если

.

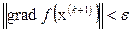В этом случае полагаем х_min = х^(k+1). Здесь

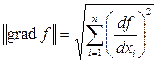
Описанный алгоритм реализован в виде подпрограммы Minim (f, xy, grad, k, h, eps), где

f – исходная функция,

xy – вектор с координатами x и y,

grad – подпрограмма, вычисляющая координаты градиента,

k – число итераций,

h – шаг,

eps – погрешность.

Задание.

Используя подпрограмму Minim, минимизировать заданную целевую функцию.