Метод Эйлера.

Пусть требуется найти приближенное решение дифференци­ального уравнения y'=f(x,у), удовлетворяющее начальному усло­вию у(х₀)=у₀. Численное решение задачи состоит в построении таблицы приближенных значений у₁, у₂,…,y_n решения уравнения у(х) в точках x₁, x₂,..., x_n. Чаще всего х_i = x₀+ih, i=1, 2,..., п. Точки x_i называются узлами сетки, а величина h—шагом (h>0).

В методе Эйлера величины у_i вычисляются по формуле

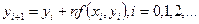(2.62)

Этот метод относится к группе одношаговых методов, в которых для расчета точки (x_i+1; .y_i+1) требуется информация только о последней вычисленной точке (x_i; y_i). Метод допускает простую геометрическую интерпретацию (рис. 15). Предположим, что известна точка (х_i; y_i) на искомой интегральной кривой. Тогда касательная к этой кривой, проходящая через точку (х_i; y_i), определяется уравнением y=y'_i(x - x_i)+y_i, а так как y'_i =f(х_i, y_i) и x_i+1=x_i+h, то y_i+1=y_i+hf(x_i, y_i). Для оценки погрешности метода на одном шаге сетки разложим точное решение в ряд Тейлора в окрестности узла х_i

Рис. 2.10

(2.63)

Сравнение формулы (2.62) с разложением (2.63) показывает, что они согласуются до членов первого порядка по h, а погрешность формулы (2.62) равна 0(h²). Если расчетные формулы численного метода согласуются с разложением в ряд Тейлора до членов порядка h^p, то число р называют порядком метода. Таким образом, метод Эйлера—метод первого порядка [10].

Для практической оценки погрешности расчета можно рекомен­довать правило Рунге. Для этого проведем вычисления с шагом h и h/2 и сравним величины у_i^(h) и у_i^(h/2). За оценку погрешности вычислений с шагом h/2 можно принять величину

.

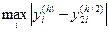Метод Эйлера легко обобщается на случай нормальных систем дифференциальных уравнений. Пусть требуется найти решение системы дифференциальных уравнений

удовлетворяющее начальным условиям y₁(x₀)= y₁₀, y₂(x₀)= y₂₀,…, y_n(x₀)= y_n0. Или в векторной форме:

,

Y(x)={y₁(x), y₂(х),...,y_n(x)}, Y₀={y₁₀, y₂₀,…, y_n0}. Приближен­ные значения у_ki точного решения y_k(х_i) в точках x_i вычисляются по формулам

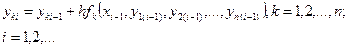
Задание:

Используя подпрограмму Eiler, составить программу решения задачи Коши y_i¢=f_i(x, y₁, y₂), y_i|_x=a = y_i(a), i = 1, 2, на отрезке [a, b].