Метод Рунге-Кутта.

Пусть требуется найти решение дифференциального уравнения y¢=f(x, y), удовлетворяющее начальному условию y(x₀) = y₀.

Численное решение задачи состоит в построении таблицы приближённых значений у₁, у₂,…,y_n решения уравнения в точках x₁, x₂,..., x_n. Точки x₁, x₂,..., x_n – узлы сетки. Используем систему равноотстоящих узлов. Величина h – шаг сетки (h>0) [10].

Методом Рунге—Кутта в литературе обычно называют од­ношаговый метод четвертого порядка, относящийся к широкому классу методов типа Рунге—Кутта. В этом методе величины y_i+1 вычисляют по следующим формулам:

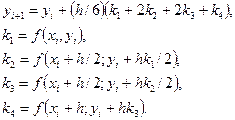(2.64)

Погрешность метода на одном шаге сетки равна Mh⁴, но на практике оце­нить величину М обычно трудно. При оценке погрешности используют пра­вило Рунге. Для этого проводят вычис­ления сначала с шагом h, а затем—с шагом h/2. Если у_i^(h) – приближение, вычисленное с шагом h, а у_2i^(h/2) – c шагом h/2, то справедлива оценка

За оценку погрешности вычислений с шагом h/2 можно принять величину

Метод Рунге—Кутта легко перено­сится на нормальные системы диф­ференциальных уравнений вида

, 1 £ k £ n,

которые для краткости удобно записы­вать в векторной форме:

y'(x)=f(x,y),

y = (y₁, y₂,…, y_n), f = (f_l,f₂,…,f_n).

Для получения расчетных формул ме­тодом Рунге—Кутта достаточно в фор­мулах (2.64) заменить у и f(x, у) соответ­ственно на у и f(x, у), а коэффициенты k_j – на k_j(j=l, 2, 3, 4).

 

Задание.

Решить задачу Коши для системы дифференциальных уравнений второго порядка. Результаты представить как и в предыдущей работе.