Решение одной из задач.

В качестве примера возьмём задачу разложения функции в ряд Тейлора (задача №1).

Поскольку ЭВМ способна непосредственно вычислять только функции, содержащие арифметические операции (полиномы, дробно-рациональные функции, полиномиальные сплайны и т.д.), то большое количество элементарных функций реализуется на вычислительной машине путём замены исходной функции её приближённым аналогом. Обычно используются полиномиальные функции: 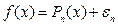. Если полная погрешность вычисления на заданном интервале не превышает заданную величину, то приближение исходной функции считается удовлетворительным.

В нашем примере с помощью арифметических операций невозможно вычислить только функцию sin(x). Разложим sin(x) в ряд Тейлора. Из курса математического анализа известно, что в окрестностях точки разложения x₀=0 функция sin(x) раскладывается в ряд Тейлора следующим образом:

,

где R_n(x) – остаточный член формулы Тейлора.

Замечание. При разложении более сложных функций в ряд Тейлора необходимо воспользоваться стандартной методикой. При этом точку разложения выбирать из соображений простоты вычисления коэффициентов формулы Тейлора и принадлежности точки разложения интервалу вычисления функции. Радиус сходимости разложения можно определить с помощью признака Даламбера, в отдельных случаях помогают признаки сходимости Коши и Лейбница.

В нашем примере остаточный член может быть оценён по формуле:

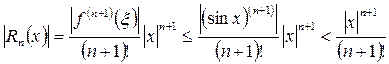
Определимся с интервалом разложения функции. Исходная функция является нечётной функцией, поскольку f(x) = -f(-x), кроме того, она терпит разрывы второго рода в точках, где sin(x) = 0. На рис. 2.11 представлен график функции:

Рис. 2.11

В точке x = 0 функция терпит устранимый разрыв первого рода, поскольку .

Будем считать, что вычисления производятся на центральном участке непрерывности функции (-π, π). Учитывая центральную симметрию функции, рассмотрим интервал (0, π). Рассмотрим, каким образом изменяется оценка остаточного члена формулы Тейлора при n = 5 (см. рис. 2.12).

Из графика видно, что при удалении x от точки разложения величина остаточного члена резко увеличивается. Установим связь между полной ошибкой приближённого представления вычисляемой функции и остаточным членом разложения sin(x) по формуле Тейлора. При замене sin(x) имеем:

.

Методическая ошибка в связи с заменой синуса полиномиальной функцией содержится в знаменателе вычисляемой функции, следовательно, по формуле оценки ошибки от деления получим:

,

учитывая, что 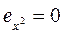имеем:

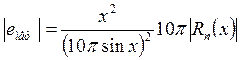
Если не учитывать погрешности округления, то для оценки числа членов ряда разложения функции sin(x), обеспечивающие заданную точность вычисления функции, можно воспользоваться неравенством:

(2.65)

В последней формуле учитывается, что в условии задачи задана величина относительной погрешности вычисления функции.

Экономизация ряда заключается в уменьшении числа арифметических операций при условии сохранения заданной точности вычисления функции. Данный приём использует свойство полиномов Чебышева сводить к минимуму максимальную ошибку приближения. Экономизация основывается на изменении структуры ряда в сторону увеличения сходимости, при этом в отдельных случаях удаётся уменьшить число членов ряда.

В нашем примере наибольшая погрешность возникает на правой границе интервала приближения функции, с другой стороны полинома Чебышева действуют на интервале (-1, 1), поэтому вычисления будем производить для x = 0,99.