Алгебра.
Одной из самых важных задач, рассматриваемых в алгебре, является нахождение корней многочленов. Пусть, например, требуется найти корни уравнения третьей степени 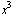 + a x + b = 0, где a и b параметры. Как известно, имеются общие формулы для корней многочленов степени не выше четвертой, содержащие арифметические операции и радикалы [13]. Воспользуемся командой Solve (Решить) для того, чтобы получить корни рассматриваемого уравнения. Команда Solve имеет два аргумента: первый - уравнение, в котором знак равенства записывается с помощью удвоенного символа =, второй - неизвестная, относительно которой решается уравнение.
+ a x + b = 0, где a и b параметры. Как известно, имеются общие формулы для корней многочленов степени не выше четвертой, содержащие арифметические операции и радикалы [13]. Воспользуемся командой Solve (Решить) для того, чтобы получить корни рассматриваемого уравнения. Команда Solve имеет два аргумента: первый - уравнение, в котором знак равенства записывается с помощью удвоенного символа =, второй - неизвестная, относительно которой решается уравнение.
Solve[x^3 + a x + b == 0, x]
Ответ записан в виде заключенных в фигурные скобки трех выражений. Каждое выражение имеет вид { x -> корень }. Его не следует понимать в том смысле, что x стремится к пределу. Символ -> используется в Математике как знак подстановки! В ответе содержится символ I - мнимая единица. Можно попытаться найти в явном виде корни некоторых полиномиальных уравнений степени выше четвертой.
Solve[x^5 + x - 1 == 0, x]
В данном случае удалось получить корни явно. Обратимся однако к следующему примеру. Пусть требуется вычислить корни многочлена пятой степени 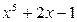 :
:
rts = Solve[x^5 + 2x - 1 == 0, x]
Подобный ответ означает, что формул для корней рассматриваемого уравнения не существует. Тем не менее, можно узнать численное значение всех пяти корней, вычислив выражение N[rts].
N[rts]
Судя по полученному ответу, рассматриваемый многочлен имеет один действительный корень, приближенно равный 0.486389, и четыре комплексных. Если желательна большая точность, ее легко можно получить, указав в качестве второго аргумента функции N число цифр в представлении результата
N[rts, 25]
Можно убедиться в правильности вычисления хотя бы одного, вещественного корня, нарисовав график многочлена 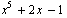 с помощью графической функции Plot
с помощью графической функции Plot
Plot[x^5+2x-1, {x, -1, 1}, AxesLabel-> {"x","y"}, AxesStyle->Thickness[0.01], PlotStyle->{Thickness[0.01],Hue[0]}, Background->GrayLevel[0.95]];
Действительно, график рассматриваемого многочлена пересекает ось Ox вблизи от точки x=0.5.
Возвращаясь к решению уравнений, заметим, что "Математика'' умеет численно решать не только полиномиальные, но и трансцендентные уравнения. Правда, если заранее известно, что какое-то уравнение имеет бесконечно много корней, следует указать хотя бы грубое приближение к искомому корню. Последнее можно найти, нарисовав график соответствующей функции. Предположим, что нам нужно найти наибольшийя корень уравнения 0.1x = Sin[x]. Поскольку 0 есть корень этого уравнения, а при x > 10 корней, очевидно, нет, нарисуем график функции 0.1x-Sin[x] на отрезке [0, 10]
Plot[0.1x - Sin[x], {x, 0, 10}, AxesStyle->Thickness[0.01], PlotStyle->{Hue[0],Thickness[0.01]}, AxesLabel->{"x","y"}, Background->GrayLevel[0.95], GridLines->Automatic];
Мы видим, что наибольший корень уравнения приближенно равен 8. Уточним его значение с помощью команды FindRoot.
FindRoot[0.1 x-Sin[x]==0, {x, 8}]
Команда Solve для уравнений с параметрами находит общее решение, которое, однако, может не иметь смысла при некоторых частных значениях параметров. Например, решения квадратного уравнения a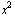 + bx + c == 0 даются формулами Виета:
+ bx + c == 0 даются формулами Виета:
Solve[a*x^2 + b* x + c == 0, x]
Эти формулы для корней не имеют смысла при a = 0. Анализ подобных случаев производит функция Reduce.
Reduce[a* x^2 + b* x + c == 0, x]
Ответ содержит логические функции && (логическое И) и ИИ (логическое ИЛИ). Проведенный анализ показывает, что при a ¹ 0, справедливы общие формулы Виета. При a = 0, b ¹ 0 решение равно - 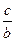 , а при a = 0, b = 0 и c = 0 любое число есть корень уравнения [13].
, а при a = 0, b = 0 и c = 0 любое число есть корень уравнения [13].
"Математика" позволяет также проводить тригонометрические преобразования. Они основаны на трактовке тригонометрических функций как рациональных функций от 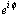 . Воспользуемся командой Simplify (Упростить) для преобразования следующего тригонометрического выражения
. Воспользуемся командой Simplify (Упростить) для преобразования следующего тригонометрического выражения
Simplify[ 6*Sin[Phi]^2 + 3*Sin[Phi]*Cos[Phi]-5*Cos[[Phi]^2]