Угол между двумя прямыми.
1). Пусть заданы две прямые:
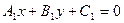 и
и 
Нормальные векторы прямых имеют координаты:

Угол между прямыми можно найти как угол между нормальными векторами:
 .
.
Условие параллельности двух прямых:
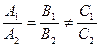 .
.
Условие перпендикулярности:
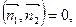 т.е.
т.е.  .
.
2). Если прямые заданы каноническими уравнениями:
 и
и 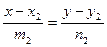 ,
,
то их направляющие векторы:  .
.
Аналогично с п.1). имеем:

Условие параллельности:
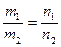 .
.
Условие перпендикулярности:
 .
.
3). Если две прямые заданы уравнениями с угловыми коэффициентами:
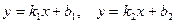 ,
,
тогда угол между прямыми можно вычислить по формуле:
 ,
,
при этом угол 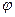 отсчитывается в направлении от первой прямой ко второй.
отсчитывается в направлении от первой прямой ко второй.
Условие параллельности:
 .
.
Условие перпендикулярности:
 .
.
Примеры:
1. Дано общее уравнение прямой:  . Напишите различные типы уравнений этой прямой.
. Напишите различные типы уравнений этой прямой.
а). Уравнение прямой в отрезках;



б). Уравнение прямой с угловым коэффициентом;

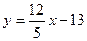
в). нормальное уравнение прямой;

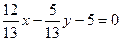 .
.
2. Найти уравнение прямой, проходящей через точку  перпендикулярно вектору
перпендикулярно вектору  .
.
Решение: Воспользуемся уравнением 

3. Составить уравнение прямой, проходящей через точку  и начало координат.
и начало координат.
Решение: Уравнение прямой, проходящей через две точки имеет вид:

4. Написать уравнение прямой с направляющим вектором 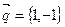 и проходящей через точку
и проходящей через точку 
Решение: 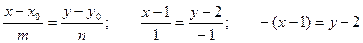
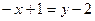
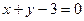
5. Найти угол между прямыми  и
и 
Решение: 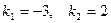

6. Показать, что прямые 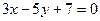 и
и 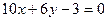 перпендикулярны.
перпендикулярны.
Решение: 
Найдём скалярное произведение 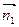 и
и 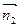
 , следовательно, прямые перпендикулярны.
, следовательно, прямые перпендикулярны.
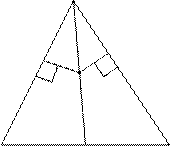
7. Даны вершины треугольника  . Найти уравнения медианы, высоты, биссектрисы, проведённых из вершины С.
. Найти уравнения медианы, высоты, биссектрисы, проведённых из вершины С.
 С
С
А Н М К В
а). медиана СМ
точка М – середина отрезка АВ.
Найдём координаты точки М:

Итак, точка 
Найдём уравнение СМ как прямой, проходящей через 2 точки М(3,3) и С(12,-1)

б). высота СН
Так как  , то вектор
, то вектор  , значит он является нормальным для прямой СН, также известны координаты точки С, через которую проходит прямая СН.
, значит он является нормальным для прямой СН, также известны координаты точки С, через которую проходит прямая СН.

в). биссектриса СК
Воспользуемся следующим свойством биссектрисы: каждая точка биссектрисы угла равноудалена от сторон этого угла.
Возьмём на биссектрисе СК текущую точку 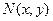 . По свойству имеем:
. По свойству имеем: 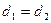 . Но
. Но 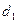 и
и  есть расстояния от точки N до АС и ВС соответственно.
есть расстояния от точки N до АС и ВС соответственно.
 C
C
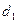

N
A K B Составим уравнения АС и ВС:
АС: 
ВС: 
Нормируем эти уравнения:
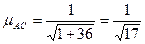 , следовательно, АС:
, следовательно, АС:  ,
,
тогда  ;
;
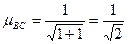 , следовательно, ВС:
, следовательно, ВС:  ,
,
тогда 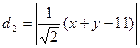 .
.
Так как 
Для того, чтобы снять модули в этом соотношении, установим положение начала координат относительно прямых АС и ВС. Так как нормали 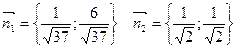 из точки О в сторону АС и ВС сонаправлены, то соотношение
из точки О в сторону АС и ВС сонаправлены, то соотношение  примет вид:
примет вид:

СК:  .
.
8. Составьте уравнения прямых, проходящих через точку  и составляющих с прямой
и составляющих с прямой  угол
угол  .
.
Будем искать уравнение прямой в виде  . Так как прямая проходит через точку А, то её координаты удовлетворяют уравнению прямой, т.е.
. Так как прямая проходит через точку А, то её координаты удовлетворяют уравнению прямой, т.е.  . Угол между прямыми, заданными уравнениями с угловыми коэффициентами можно найти по формуле:
. Угол между прямыми, заданными уравнениями с угловыми коэффициентами можно найти по формуле:
 .
.
Так как угловой коэффициент данной прямой равен  , а угол
, а угол  , то
, то 
Имеем два значения k:
 .
.
Найдём соответствующие значения b: 
Получили две искомые прямые:  .
.
9. Прямая отсекает на координатных осях равные положительные отрезки. Составить уравнение прямой, если площадь треугольника, образованного прямой и осями координат равна 8.
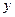 Будем искать уравнение прямой в отрезках
Будем искать уравнение прямой в отрезках
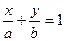 , так как
, так как  , то
, то 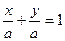
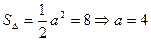
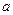
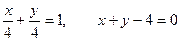

10. При каких значениях параметра t прямые 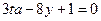 и
и  параллельны?
параллельны?
Прямые, заданные общими уравнениями параллельны, если коэффициенты при x и y пропорциональны, т.е.
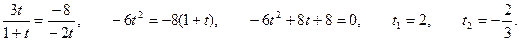
11. Найти уравнение общей хорды двух окружностей: 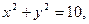

Решение: Найдём точки пересечения окружностей, для этого решим систему уравнений:

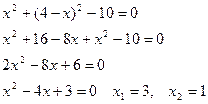
Соответственно,  .
.
Теперь получим уравнение общей хорды, зная две точки  , через которые проходит эта прямая:
, через которые проходит эта прямая:

12. Найти расстояние от точки  до прямой
до прямой  .
.
Решение: Нормируем уравнение прямой  .
.
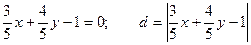
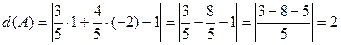 .
.