Прямая в пространстве.
Прямая в пространстве может быть задана:
1). Общими уравнениями
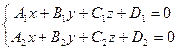 ,
,
что равносильно её заданию как линии пересечения двух плоскостей;
2). Каноническим уравнением
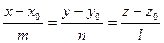 ,
,
прямая проходит через точку  параллельно направляющему вектору
параллельно направляющему вектору  ;
;
3). Параметрическими уравнениями
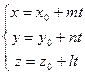 .
.
Заметим, что направляющий вектор прямой 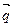 можно найти как векторное произведение нормальных векторов
можно найти как векторное произведение нормальных векторов 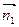 и
и 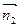 , т.е.
, т.е.
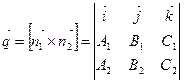 .
.
Угол между прямыми есть угол между направляющими векторами
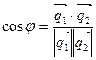 .
.
Угол между прямой  и плоскостью
и плоскостью 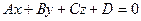 определяется по формуле:
определяется по формуле:
 .
.
Условие параллельности прямой и плоскости: 
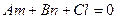 .
.
Условие перпендикулярности прямой и плоскости: 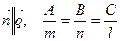 .
.
Условие принадлежности двух прямых одной плоскости. Пусть прямые заданы каноническими уравнениями:
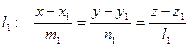 и
и  .
.
Две прямые лежат в одной плоскости, если компланарны векторы 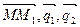 , т.е. их смешанное произведение равно 0, т.е.
, т.е. их смешанное произведение равно 0, т.е.
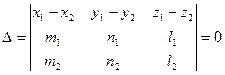 .
.
Если 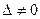 , то прямые являются скрещивающимися.
, то прямые являются скрещивающимися.
Примеры:
1. Составьте уравнение плоскости, зная что точка  служит основанием перпендикуляра, проведённого из начала координат к этой плоскости.
служит основанием перпендикуляра, проведённого из начала координат к этой плоскости.
Решение: По условию задачи вектор 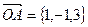 является нормальным вектором плоскости и точка
является нормальным вектором плоскости и точка  принадлежит плоскости.
принадлежит плоскости.
Воспользуемся уравнением:
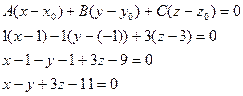
2. Найти уравнение плоскости, проходящей через две точки:  и
и 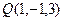 и перпендикулярной плоскости
и перпендикулярной плоскости  .
.
Решение: Вектор нормали к плоскости  параллелен искомой плоскости.
параллелен искомой плоскости.
Выберем на плоскости текущую точку 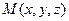 . Векторы
. Векторы  - компланарны. Тогда
- компланарны. Тогда

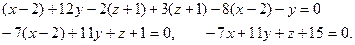
3. Составьте уравнение плоскости, проходящей через ось  и образующей с плоскостью
и образующей с плоскостью 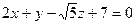 угол
угол 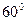 .
.
Решение: Плоскость, проходящая через ось  задаётся уравнением
задаётся уравнением  , где А и В одновременно в ноль не обращаются. Пусть
, где А и В одновременно в ноль не обращаются. Пусть 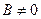 , тогда
, тогда 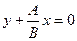 . Обозначим
. Обозначим 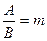 , тогда уравнение плоскости примет вид
, тогда уравнение плоскости примет вид 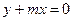 .
.
Нормальный вектор данной плоскости 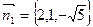 , искомой плоскости
, искомой плоскости 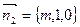 .
.
По формуле косинуса угла между двумя плоскостями имеем:

 .
.
Откуда получаем две плоскости: 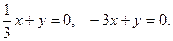
4. В пучке, определяемом плоскостями 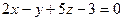 и
и 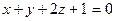 , найти две перпендикулярные плоскости, одна из которых проходит через точку
, найти две перпендикулярные плоскости, одна из которых проходит через точку  .
.
Решение: Уравнение пучка плоскостей имеет вид:
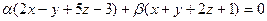 или
или
 .
.
Для того, чтобы выделить из пучка плоскость, проходящую через точку М, подставим координаты этой точки в уравнение пучка
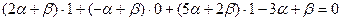
откуда имеем 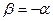 .
.
Тогда уравнение плоскости, содержащей точку М, найдём, подставив соотношение 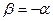 в уравнение пучка
в уравнение пучка
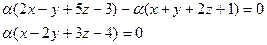
Так как  (иначе
(иначе 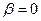 , а это противоречит определению пучка), то имеем уравнение:
, а это противоречит определению пучка), то имеем уравнение: 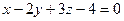 .
.
Вторая плоскость, принадлежащая пучку, должна быть ей перпендикулярна. Запишем условие ортогональности нормальных векторов:
 .
.
Значит, уравнение второй плоскости имеет вид:
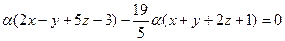
или (в силу того, что  )
) 
5. Даны координаты вершин пирамиды 
Найти угол между ребром  и гранью
и гранью  .
.
Решение: Найдём вектор нормали к грани  , как векторное произведение
, как векторное произведение 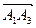 и
и  .
.


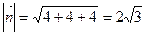 .
.
Найдём координаты вектора 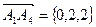 .
.
Найдём угол 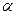 между вектором нормали и
между вектором нормали и 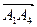 :
:
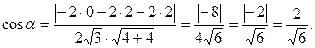
Искомый угол между вектором и плоскостью равен  .
.
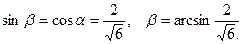
6. Даны плоскость 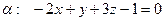 , прямая
, прямая  и точка
и точка 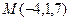 .
.
а). Составить уравнение плоскости, проходящей через точку М и параллельной плоскости 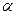 .
.
В качестве вектора нормали к искомой плоскости можно взять 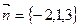 - нормаль
- нормаль 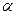 . Поэтому уравнение плоскости будет иметь вид:
. Поэтому уравнение плоскости будет иметь вид: 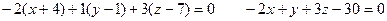 .
.
б). Составить уравнение прямой, проходящей через точку М и параллельной  . В качестве направляющего вектора искомой прямой можно взять
. В качестве направляющего вектора искомой прямой можно взять  - направляющий вектор
- направляющий вектор  . Тогда уравнение прямой:
. Тогда уравнение прямой: 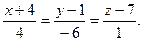
в). Составить уравнение плоскости, проходящей через точку М и перпендикулярной  .
.
В качестве вектора нормали к исходной плоскости можно взять  - направляющий вектор
- направляющий вектор  и уравнение плоскости будет
и уравнение плоскости будет 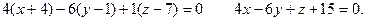
г). Составить уравнение прямой, проходящей через точку М и перпендикулярной 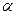 .
.
Направляющим вектором искомой прямой можно взять 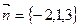 - нормаль
- нормаль 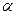 . Отсюда получим уравнение прямой
. Отсюда получим уравнение прямой 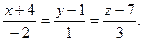
д). Составить уравнение плоскости, проходящей через точку М и прямую  .
.
Запишем уравнение  в параметрической форме:
в параметрической форме: 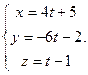 Придав
Придав 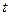 два различных значения, например,
два различных значения, например,  найдём две точки прямой.
найдём две точки прямой.


Точки  принадлежат искомой плоскости. Составим уравнение плоскости, проходящей через три точки:
принадлежат искомой плоскости. Составим уравнение плоскости, проходящей через три точки:
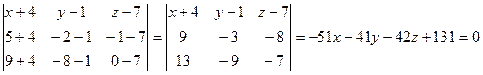 .
.
е). Составить уравнение плоскости, проходящей через точку М и перпендикулярной плоскостям 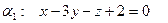 и
и 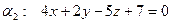 .
.
В качестве нормального вектора искомой плоскости можно взять векторное произведение  и
и 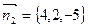 - нормальных векторов
- нормальных векторов 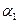 и
и  .
.
 .
.
Зная точку М, через которую проходит плоскость, и вектор нормали 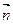 , составим уравнение искомой плоскости:
, составим уравнение искомой плоскости:
 .
.
ж). Найти точку пересечения прямой  и плоскости
и плоскости 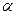 .
.
Воспользуемся параметрическими уравнениями прямой  .
.

Подставим эти уравнения в уравнение плоскости 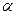 .
.
 .
.
Подставим найденное значение t в параметрические уравнения прямой
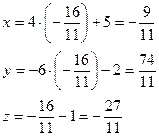
Таким образом, точка пересечения прямой и плоскости 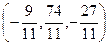
з). Найти расстояние от точки М до плоскости 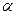 .
.
Нормируем уравнение плоскости 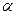
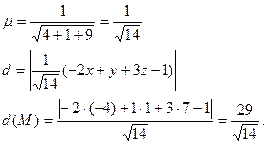
7. Найти каноническое уравнение прямой, если она задана в виде:

Решение: Чтобы составить каноническое уравнение нужно знать точку, через которую проходит эта прямая и направляющий вектор.
Для нахождения произвольной точки прямой примем её координату  (можно взять любое другое значение) и подставим в систему
(можно взять любое другое значение) и подставим в систему
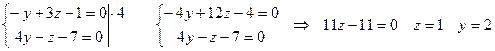
Итак, точка 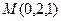 .
.
Прямая задана как пересечение плоскостей, векторы нормалей  и
и  перпендикулярны прямой. Поэтому в качестве направляющего вектора
перпендикулярны прямой. Поэтому в качестве направляющего вектора 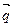 можно взять векторное произведение
можно взять векторное произведение 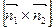
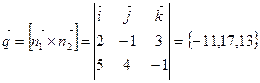 .
.
Тогда каноническое уравнение прямой:
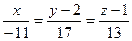 .
.
8. Найти расстояние от точки 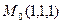 до прямой
до прямой  :
: 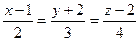 .
.

 Составим уравнение плоскости
Составим уравнение плоскости 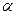 ,
,
проходящей через точку 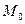 перпенди-
перпенди-
кулярно  .
.
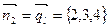
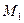
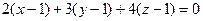
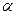
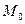
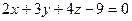
Найдём точку 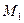 пересечения прямой
пересечения прямой  и плоскости
и плоскости 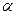 .
.
Перейдём к параметрическим уравнениям прямой  :
:
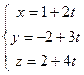
Подставим их в уравнение плоскости:
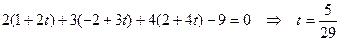
Таким образом, точка 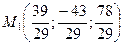 .
.
Искомое расстояние 
ТЕМА 3. ВВЕДЕНИЕ В МАТЕМАТИЧЕСКИЙ АНАЛИЗ.