Системы линейных уравнений
Системой линейных уравнений (СЛУ) называется система уравнений вида:

Система называется однородной, если 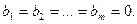
Матрица  называется матрицей коэффициентов.
называется матрицей коэффициентов.
Матрица 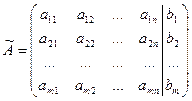 называют расширенной матрицей системы.
называют расширенной матрицей системы.
Столбец 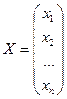 называют столбцом неизвестных.
называют столбцом неизвестных.
Столбец  называют столбцом свободных членов.
называют столбцом свободных членов.
С учётом этих обозначений можно записать систему в матричной форме
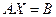 .
.
Рассмотрим отдельно случай квадратной системы, когда  , и общий случай, когда
, и общий случай, когда 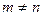 .
.
1) Квадратная система
Пусть дана СЛУ, в которой  и
и  .
.
Существуют три основных метода решения СЛУ:
а) метод Крамера
б) метод обратной матрицы
в) метод Гаусса
а) Обозначим
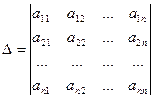


(определитель 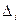 получается из
получается из 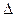 заменой i-го столбца на столбец свободных членов)
заменой i-го столбца на столбец свободных членов)
Тогда 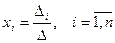
б) Рассмотрим СЛУ в матричной форме
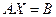
Домножим слева на 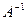

Но произведение 
Таким образом

в) При решении СЛУ методом Гаусса, расширенную матрицу системы приводят к треугольному виду с помощью элементарных преобразований

По данной матрице составляется система

Из последнего равенства найдём 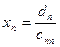 и подставим его в предыдущее
и подставим его в предыдущее
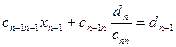
Из этого равенства найдём  и подставим в предыдущее и т.д.
и подставим в предыдущее и т.д.
2) Общий случай
Теорема Кронекера-Капелли
Система линейных уравнений совместна тогда и только тогда, когда
 .
.
В случае, когда число уравнений не равно числу неизвестных, систему удобно решать методом Гаусса, который состоит в приведении расширенной матрицы к трапецеидальному виду путём применения элементарных преобразований. Если при этом на некотором этапе получается строка, в которой все элементы, кроме столбца свободных членов, равны нулю, то система несовместна (это случай, когда 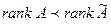 ). Если
). Если 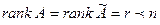 , то система имеет бесконечно много решений, и каждое решение зависит от
, то система имеет бесконечно много решений, и каждое решение зависит от  не зависящих друг от друга параметров, т.е. степень свободы системы
не зависящих друг от друга параметров, т.е. степень свободы системы  . В качестве параметров удобно брать «лишние неизвестные», которые объявляются свободными, остальные переменные – базисные выражаются через свободные.
. В качестве параметров удобно брать «лишние неизвестные», которые объявляются свободными, остальные переменные – базисные выражаются через свободные.
Однородная система линейных уравнений
Расширенная матрица отличается от матрицы коэффициентов наличием нулевого столбца, т.е.  . Значит, по теореме Кронекера-Капелли система всегда совместна. Одно решение очевидно -
. Значит, по теореме Кронекера-Капелли система всегда совместна. Одно решение очевидно -  . Это решение называется тривиальным. Если
. Это решение называется тривиальным. Если 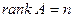 , то решение единственное – тривиальное, если
, то решение единственное – тривиальное, если 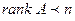 , то решений бесконечно много.
, то решений бесконечно много.
Обозначим базисные неизвестные 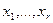 , тогда
, тогда

В матричной форме
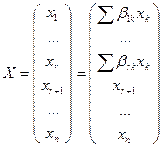
Можно записать так:
 , где
, где

Решение 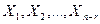 называется фундаментальной системой решений (ФСР) однородной системы. Общее решение системы является линейной комбинацией фундаментальной системы решений.
называется фундаментальной системой решений (ФСР) однородной системы. Общее решение системы является линейной комбинацией фундаментальной системы решений.
