Векторы. Основные определения.
Вектором называется направленный отрезок. К векторам относится также нулевой вектор, начало и конец которого совпадают. Вектор характеризуется своей длиной (модулем) и направлением.
 B
B
A
Линейные операции над векторами:
1). Сложение векторов.

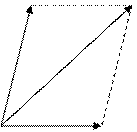 |

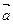
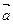
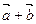
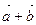

Складывают два вектора по правилу параллелограмма или треугольника. Правило треугольника можно обобщить на n-слагаемых. Если каждый раз соединять начало последующего вектора с концом предыдущего, то получим ломаную линию. Вектор, соединяющий начало первого с концом последнего и есть сумма.
2). Умножение вектора на число.
При умножении вектора 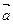 на число
на число 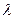 его модуль увеличивается (если
его модуль увеличивается (если  ) или уменьшается (если
) или уменьшается (если 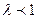 ) в
) в 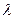 раз, а направление не изменяется, если
раз, а направление не изменяется, если 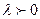 и меняется на противоположное, если
и меняется на противоположное, если 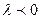 .
.
В любом случае векторы 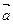 и
и 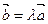 лежат на одной прямой или на параллельных прямых. Такие векторы называются коллинеарные.
лежат на одной прямой или на параллельных прямых. Такие векторы называются коллинеарные.
Нулевой вектор считается коллинеарным любому вектору.
Векторы, лежащие в одной плоскости или в параллельных плоскостях, называются компланарными.
Свойства линейных операций:
1). Коммутативность
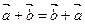
2). Ассоциативность
 ,
, 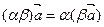
3). Дистрибутивность
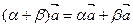
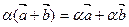 , где
, где 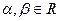
Рассмотрим систему векторов  . Выражение вида
. Выражение вида  , где
, где 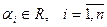 называется линейной комбинацией векторов
называется линейной комбинацией векторов 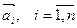 . Если в линейной комбинации все
. Если в линейной комбинации все  , то система векторов линейно независима. Если существуют
, то система векторов линейно независима. Если существуют 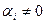 , то система – линейно зависима.
, то система – линейно зависима.
Любая упорядоченная линейно независимая тройка векторов  называется базисом в пространстве. Векторы
называется базисом в пространстве. Векторы  называются базисными. Если базисные вектора взаимно перпендикулярны, то базис называется ортогональным. Если базисные векторы имеют единичную длину, то они называются ортами. Базис называется ортонормированным, если базисные векторы единичные и взаимно перпендикулярные. Декартова система координат – ортонормированная, орты прямоугольной декартовой системы координат обозначают
называются базисными. Если базисные вектора взаимно перпендикулярны, то базис называется ортогональным. Если базисные векторы имеют единичную длину, то они называются ортами. Базис называется ортонормированным, если базисные векторы единичные и взаимно перпендикулярные. Декартова система координат – ортонормированная, орты прямоугольной декартовой системы координат обозначают  .
.
Пусть  - некоторый базис в пространстве. Пусть
- некоторый базис в пространстве. Пусть 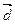 - произвольный вектор пространства. Рассмотрим линейную комбинацию
- произвольный вектор пространства. Рассмотрим линейную комбинацию
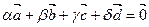
Так как любая четвёрка векторов линейно зависима, то не все коэффициенты линейной комбинации равны 0.
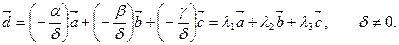
Эта формула даёт разложение вектора 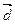 по базису (
по базису ( ). Коэффициенты
). Коэффициенты 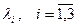 - координаты вектора
- координаты вектора 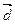 в этом базисе. Разложение вектора по базису единственное, т.е. координаты вектора однозначно определяют сам вектор.
в этом базисе. Разложение вектора по базису единственное, т.е. координаты вектора однозначно определяют сам вектор.
В связи с этим можно записать следующие свойства:
Пусть даны векторы 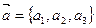 и
и 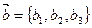
1). Равные векторы имеют одинаковые координаты, т.е. если 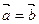 , то
, то 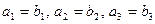 .
.
2). При умножении вектора на число, его координаты умножаются на это число 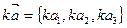 .
.
3). При сложении двух векторов складываются их соответствующие координаты 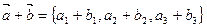 .
.
Проекцией вектора 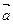 на вектор
на вектор  называется число
называется число  , где
, где 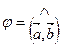 .
.
Координаты вектора 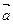 в прямоугольном базисе совпадают с проекциями вектора
в прямоугольном базисе совпадают с проекциями вектора 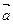 на базисные орты
на базисные орты  , а длина вектора равна
, а длина вектора равна
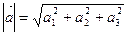
Числа 
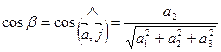

называются направляющими косинусами вектора 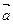 .
.