Однородные дифференциальные уравнения.

Уравнения вида называется однородным уравнением.

Однородное уравнение приводится к уравнению с разделяющимися переменными подстановкой y=Ux, где U- новая искомая функция. Дифференцируя равенство y=Ux, получим

.

Подставив выражения y и в уравнение, имеем

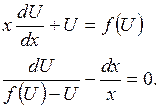
Это уже уравнение с разделяющимися переменными, найдя его общее решение и заменив U на 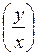, получим общее решение исходного уравнения.

Например.

1). Найти общее решение дифференциального уравнения

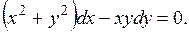
Запишем уравнение следующим образом

.

Поделим числитель и знаменатель на х²:

, (*)

т.е. получим y как функцию от . Это означает, что данное уравнение однородное. Для решения этого уравнения введем новую функцию U=.

Тогда

y=Ux, .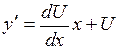

Используя замену запишем уравнение (*) в виде:

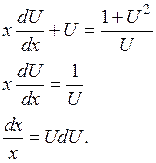
Интегрируя последнее выражение, получим

Заменяя в полученном равенстве U отношением , окончательно имеем

.

 

Найти общее решение дифференциальных уравнений:

6.18.	.	6.19.	.
6.20.	.	6.21.	.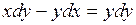

Найти частное решение дифференциальных уравнений:

6.22.

6.23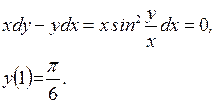

6.24.

 

6.25

.