Дифференцирование сложной функции.

 

Пусть 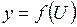и - дифференцируемые функции. Тогда сложная функция есть также дифференцируемая функция, причем

.

Это правило распространяется на цепочку из любого конечного числа дифференцируемых функций: производная сложной функции равна произведению производных функций, ее составляющих.

Рассмотрим несколько примеров нахождения производной сложной функции.

Пример 1.

Положим , где .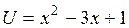

Тогда

.

 

Пример 2.

.

Обозначим . Тогда .

По правилу дифференцирования сложной функции имеем:

.

 

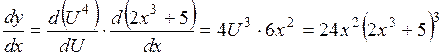Пример 3.

.

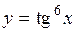Обозначим 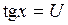. Тогда .

По правилу дифференцирования сложной функции имеем:

=.

 

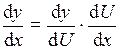Пример 4.

.

Положим . Тогда .

.

 

Пример 5.

.

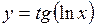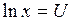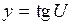Если , то . Следовательно

.

 

Пример 6.

.

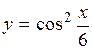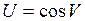Положим , где , а .

Получаем

=.

 

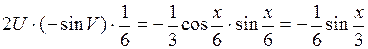Пример 7.

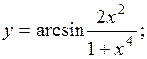
<1.

Если то , следовательно,

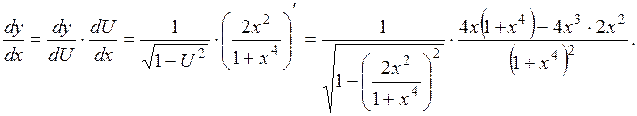Выполним алгебраические преобразования и получим окончательно

.

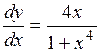Пример 8.

Имеем

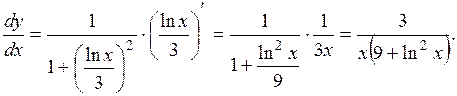
Найти производные следующих сложных функций:

 

2.81.	(Ответ: 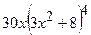)	2.82.	(Ответ: )
2.83.	(Ответ: )	2.84.	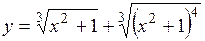(Ответ: )
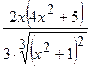2.85.	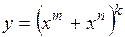(Ответ: 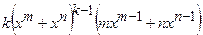)	2.86.	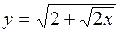(Ответ: )

2.87.	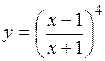(Ответ: 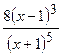)	2.88.	(Ответ: )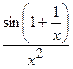
2.89.	(Ответ: 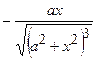)	2.90.	(Ответ: )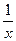
2.91.	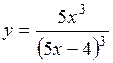(Ответ: 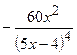)	2.92.	(Ответ: )
2.93.	(Ответ: 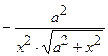)	2.94.	(Ответ: )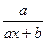
2.95.	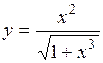(Ответ: 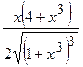)	2.96.	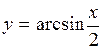(Ответ: )
2.97.	(Ответ: 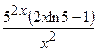)	2.98.	(Ответ: )
2.99.	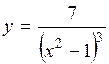(Ответ: )	2.100.	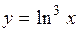(Ответ: )
2.101.	(Ответ: )	2.102.	(Ответ: )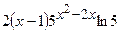
2.103.	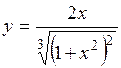(Ответ: )	2.104.	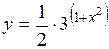(Ответ: )
2.105.	(Ответ: 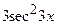)	2.106.	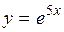(Ответ: )
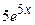2.107.	(Ответ: 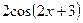)	2.108.	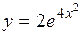(Ответ: )
2.109.	(Ответ: 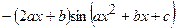)	2.110.	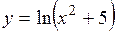(Ответ: )
2.111.	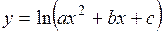(Ответ: 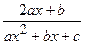)	2.112.	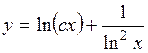(Ответ: )
2.113.	(Ответ: 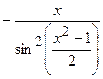)	2.114.	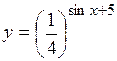(Ответ: )
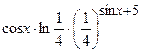2.115.	(Ответ: 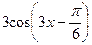)	2.116.	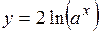(Ответ: )
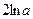2.117.	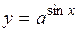(Ответ: 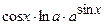)	2.118.	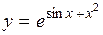(Ответ: )
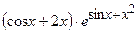2.119.	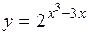(Ответ: 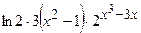)	2.120.	(Ответ: )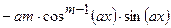
2.121.	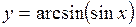(Ответ: )	2.122.	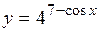(Ответ: )
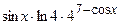2.123.	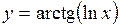(Ответ: 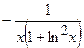)	2.124.	(Ответ: )
2.125.	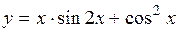(Ответ: )	2.126.	(Ответ: )