Определенный интеграл
Пусть функция  задана на отрезке
задана на отрезке 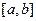 . Разобьем отрезок
. Разобьем отрезок 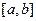 на
на 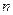 элементарных отрезков точками
элементарных отрезков точками 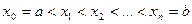 .
.
В каждом из отрезков разбиения  выберем произвольно точку
выберем произвольно точку  и положим
и положим 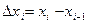 . Тогда сумма вида
. Тогда сумма вида
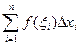
называется интегральной суммой для функции  на отрезке
на отрезке 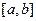 .
.
Пусть существует и конечен предел S интегральной суммы при стремлении к нулю длины максимального элементарного отрезка 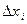 , не зависящий от способа разбиения отрезка
, не зависящий от способа разбиения отрезка 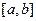 на части и способа выбора точек
на части и способа выбора точек  на отрезках разбиения. Тогда функция
на отрезках разбиения. Тогда функция  называется интегрируемой на
называется интегрируемой на 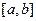 , а число S – определенным интегралом от
, а число S – определенным интегралом от 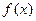 на
на 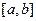 и обозначается
и обозначается 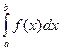 .
.
Свойства определенного интеграла
1) 
2) 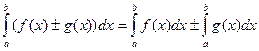
3) 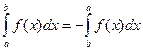
4) 
5) 
6)  , если функция
, если функция  четная
четная
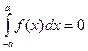 , если функция
, если функция  нечетная
нечетная
7) Формула Ньютона-Лейбница

Геометрические приложения определенного интеграла
1. Если функция  неотрицательна на отрезке
неотрицательна на отрезке 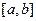 , то площадь S под кривой
, то площадь S под кривой  на
на 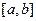 (площадь криволинейной трапеции, ограниченной кривой
(площадь криволинейной трапеции, ограниченной кривой  и прямыми
и прямыми 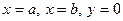 ) численно равна определенному интегралу от
) численно равна определенному интегралу от 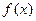 на данном отрезке:
на данном отрезке:
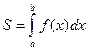
(геометрический смысл определенного интеграла)
2. Если функция  неположительна на отрезке
неположительна на отрезке 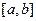 , то площадь S над кривой
, то площадь S над кривой  на
на 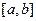 численно равна определенному интегралу от
численно равна определенному интегралу от 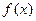 на данном отрезке, взятому со знаком «минус»:
на данном отрезке, взятому со знаком «минус»:

3. Если  на отрезке
на отрезке 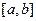 , то площадь S фигуры, заключенной между кривыми
, то площадь S фигуры, заключенной между кривыми  и
и 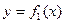 на этом отрезке определяется формулой
на этом отрезке определяется формулой
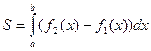 .
.