Дифференциальное исчисление функций нескольких переменных
Дифференциальное исчисление функций двух переменных
Определение. Частными производными в точке 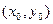 по
по 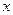 и
и 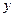 называют соответственно
называют соответственно 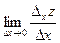 и
и  .
.
Обозначения:  ,
,  или
или 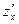 ,
,  , или
, или  ,
,  или
или  ,
, 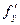 .
.
Пример. 
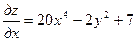 ,
, 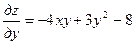 .
.
Определение. Выражение вида
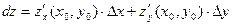
называется полным дифференциалом функции в точке 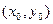 .
.
Производная по направлению  определяет скорость изменения функции в этом направлении и вычисляется следующим образом:
определяет скорость изменения функции в этом направлении и вычисляется следующим образом:
 ,
,
где  - угол между вектором
- угол между вектором  и осью ОХ.
и осью ОХ.
Градиент функции 
В каждой точке  области D, где задана функция
области D, где задана функция  (скалярное поле), определим вектор
(скалярное поле), определим вектор  , координатами которого будут частные производные
, координатами которого будут частные производные 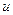 , вычисленные в этой точке:
, вычисленные в этой точке: 
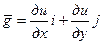 .
.
Вектор  называется градиентом функции, и обозначают
называется градиентом функции, и обозначают  .
.
Экстремумы функции нескольких переменных
Функция 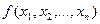 в точке
в точке 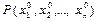 имеет максимум, если в любой точке
имеет максимум, если в любой точке 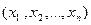 достаточно малой
достаточно малой  - окрестности точки Р выполняется неравенство:
- окрестности точки Р выполняется неравенство:
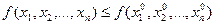 ,
,
и минимум, если  .
.
Теорема (необходимый признак экстремума функции 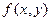 ).
).
Если в точке экстремума 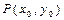 функция
функция 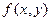 имеет частные производные первого порядка, то они равны нулю:
имеет частные производные первого порядка, то они равны нулю:
 .
.
Теорема (достаточный признак экстремума функции 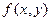 ).
).
Пусть в некоторой внутренней точке 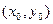 области D функция
области D функция 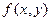 имеет непрерывные частные производные до третьего порядка включительно. Если выполнены равенства
имеет непрерывные частные производные до третьего порядка включительно. Если выполнены равенства  и выражение:
и выражение:
 ,
,
то в точке 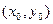 - экстремум. При этом если
- экстремум. При этом если  , то в точке
, то в точке 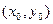 - максимум, если
- максимум, если 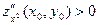 , то в точке
, то в точке 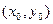 - минимум.
- минимум.
Пример. Найти экстремумы функции 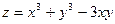 .
.
Решение. 1) Составим и решим систему уравнений
 ;
; 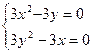 ;
; 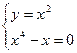 ;
; 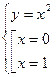 ;
;  .
.
Таким образом, получили две точки, «подозрительные» на экстремум:
 и
и 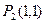 .
.
2) Вычислим вторые производные данной функции:

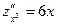 ,
, 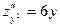 ,
, 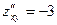 .
.
Найдем значения этих производных в точках  и
и 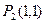 :
:
а)  :
: 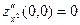 ,
,  ,
, 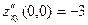 . Тогда
. Тогда 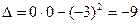 .
.
Таким образом, точка  не является экстремумом функции
не является экстремумом функции 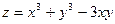 .
.
б) 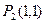 :
:  ,
,  ,
,  . Тогда
. Тогда  .
.
Таким образом, точка 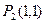 является экстремумом функции
является экстремумом функции 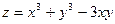 , а именно минимумом функции, так как
, а именно минимумом функции, так как  .
.