Комплексные числа и действия над ними
Определение. Комплексным числом 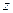 называется выражение
называется выражение 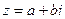 , где
, где 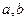 - действительные числа, а
- действительные числа, а 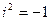 ;
; 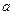 называется действительной (вещественной) частью комплексного числа
называется действительной (вещественной) частью комплексного числа 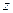 (
(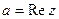 );
); 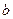 - мнимая часть комплексного числа
- мнимая часть комплексного числа 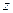 (
(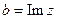 ).
).
Два комплексных числа 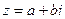 и
и  отличающиеся только знаком мнимой части, называются комплексно сопряженными.
отличающиеся только знаком мнимой части, называются комплексно сопряженными.
Числа 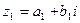 и
и 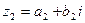 равны (
равны (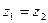 ), если
), если 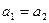 и
и 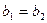 .
.
Для геометрического изображения комплексного числа введем понятие комплексной плоскости. На плоскости ХОУ комплексное число 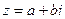 изображается точкой
изображается точкой 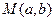 (или вектором
(или вектором 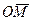 ); ось ОХ называется действительной осью, а ось ОУ – мнимой.
); ось ОХ называется действительной осью, а ось ОУ – мнимой.
Действия над комплексными числами
1. Суммой двух комплексных чисел 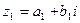 и
и 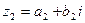 называется комплексное число
называется комплексное число  .
.
2. Разностью двух комплексных чисел 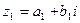 и
и 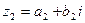 называется комплексное число
называется комплексное число 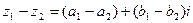 .
.
3. Чтобы найти произведение двух комплексных чисел 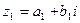 и
и 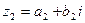 , следует перемножить их по обычным правилам алгебры, учитывая, что
, следует перемножить их по обычным правилам алгебры, учитывая, что 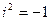 :
:
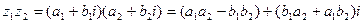 .
.
Заметим, что произведение двух сопряженных чисел – неотрицательное действительное число:
 .
.
4. Для деления комплексных чисел 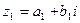 и
и 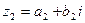 (
(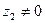 ) надо домножить числитель и знаменатель на число, сопряженное знаменателю:
) надо домножить числитель и знаменатель на число, сопряженное знаменателю:
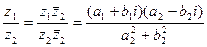
Тригонометрическая форма комплексного числа
Обозначим через 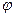 и
и 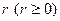 полярные координаты точки
полярные координаты точки 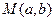 . Тогда
. Тогда 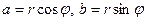 и
и 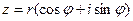 - тригонометрическая форма комплексного числа. Число
- тригонометрическая форма комплексного числа. Число 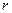 называется модулем, а
называется модулем, а 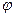 - аргументом комплексного числа
- аргументом комплексного числа 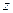 :
:  , при этом
, при этом
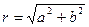 ,
,  ,
,  ,
, 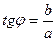 .
.
Формула Муавра для возведения комплексного числа 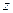 в степень:
в степень:
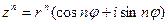 .
.
Формула корня n-й степени из комплексного числа:
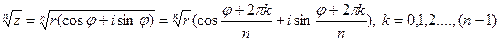 .
.