Дифференциальные уравнения первого порядка
Определение. Дифференциальным уравнением (д.у.) называется уравнение, содержащее производные неизвестной функции.
Если неизвестная функция зависит только от одного переменного, то д.у. называется обыкновенным; если от нескольких переменных и производные, входящие в д.у. – частные, то дифференциальным уравнением с частными переменными.
Так как наиболее частным случаем является изучение тех или иных характеристик процессов, протекающих во времени, то независимую переменную в обыкновенном д.у. будем обозначать через t, а функцию через х.
Наивысший порядок производной неизвестной функции, входящей в д.у. называется порядком дифференциального уравнения.
Решением дифференциального уравнения называется функция, при подстановке которой д.у. обращается в тождество.
Общий вид д.у. первого порядка есть
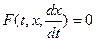 .
.
Задача Коши для д.у. первого порядка, разрешенного относительно производной:
найти определенную на некотором интервале  функцию
функцию  , имеющую на
, имеющую на  производную
производную  такую, что
такую, что
 для всех
для всех 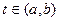
и удовлетворяющую условию
 ,
,
где 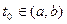 , а в точке
, а в точке  определена функция
определена функция  .
.
Значения  ,
, 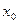 при этом называются начальными данными, а условие
при этом называются начальными данными, а условие  - начальным условием.
- начальным условием.
Итак, задача Коши для д.у. состоит в нахождении решения д.у., удовлетворяющего заданному начальному условию.
Виды дифференциальных уравнений первого порядка
1. Дифференциальные уравнения с разделенными переменными
Уравнение вида

называется дифференциальным уравнением первого порядка с разделенными переменными.
Пример. Решить дифференциальное уравнение
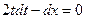 .
.
Решение.
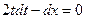 ;
;
 ;
;
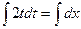 ;
;
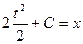 ;
;
 .
.
2. Дифференциальные уравнения с разделяющимися переменными
Уравнение вида

называется дифференциальным уравнением первого порядка с разделяющимися переменными.
Разделим обе части д.у. на 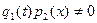 , получим уравнение
, получим уравнение
 ,
,
которое является уравнением с разделенными переменными.
Пример. Решить дифференциальное уравнение
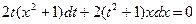 .
.
Решение.
Разделим обе части уравнения на  , получим
, получим
 ;
;
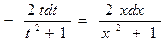 ;
;
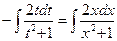 ;
;
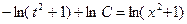 ;
;
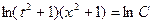 ;
;
 .
.
3. Однородные уравнения первого порядка
Уравнение вида
 ,
,
где  - однородная функция нулевого измерения, называется однородным д.у. первого порядка.
- однородная функция нулевого измерения, называется однородным д.у. первого порядка.
Заменой  ,
, 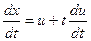 д.у. сводится к уравнению с разделяющимися переменными.
д.у. сводится к уравнению с разделяющимися переменными.
Пример. Решить дифференциальное уравнение
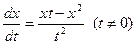 .
.
Решение.
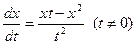 ;
;
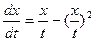 .
.
Сделаем замену  ,
, 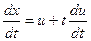 , получим
, получим
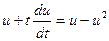 ;
;
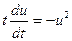 .
.
Разделим обе части уравнения на  , получим
, получим
 ;
;
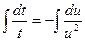 ;
;
 ;
;
 ;
;
 .
.
Тогда, 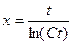 .
.
4. Уравнение Бернулли
Уравнение вида
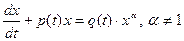
называется уравнением Бернулли.
Для решения уравнения делают замену
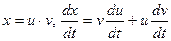 .
.
Тогда уравнение Бернулли примет вид
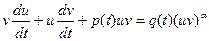 ;
;
 .
.
Найдем  из решения уравнения
из решения уравнения 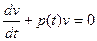 ,
, 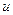 найдем из решения уравнения
найдем из решения уравнения 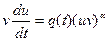 .
.
Пример. Решить дифференциальное уравнение
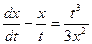
Решение. Сделаем замену 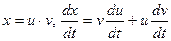 , получим
, получим
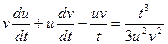 ;
;
 .
.
1) решим уравнение
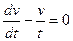 ;
;
 ;
;
 ;
;
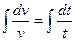 ;
;
 ;
;

2) решим уравнение
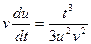 ;
;
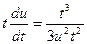 ;
;
 ;
;
 ;
;
 ;
;
 ;
;
 ;
;
 ;
;

Тогда,  .
.
5. Линейное уравнение первого порядка
Уравнение Бернулли при 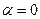 , т.е. дифференциальное уравнение вида
, т.е. дифференциальное уравнение вида

называется линейным уравнением первого порядка.
 Замена и метод решения линейного д.у. первого порядка аналогичны замене и методам решения уравнения Бернулли.
Замена и метод решения линейного д.у. первого порядка аналогичны замене и методам решения уравнения Бернулли.
Пример. Решить дифференциальное уравнение
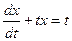 .
.
Решение. Сделаем замену 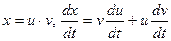 , получим
, получим
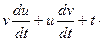
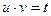 ;
;

 ;
;
1) Решим уравнение  ;
;
 ;
;
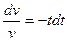 ;
;
 ;
;
 ;
;
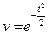
2) Решим уравнение 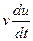
 ;
;
 ;
;
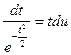 ;
;
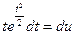 ;
;
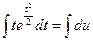 ;
;
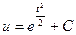 .
.
Тогда, решением д.у. является функция 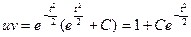 .
.