Дифференциальные уравнения второго порядка
Очень важным классом дифференциальных уравнений порядка выше первого вляется класс линейных дифференциальных уравнений.
Рассмотрим линейные дифференциальные уравнения второго порядка. Прежде всего, остановимся на изучении однородных линейных дифференциальных уравнениях второго порядка.
Уравнение вида
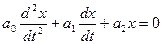
называется однородным линейным дифференциальным уравнением второго порядка.
В дальнейшем будем предполагать коэффициенты  данного уравнения непрерывными на некотором интервале
данного уравнения непрерывными на некотором интервале  оси
оси 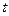 функциями.
функциями.
Дифференциальному уравнению ставится в соответствие характеристическое уравнение:

1) Если характеристическое уравнение имеет два различных действительных корня 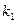 и
и 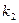 , то общее решение уравнения имеет вид:
, то общее решение уравнения имеет вид:
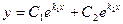
2) Если характеристическое уравнение имеет один действительный корень (кратности 2), то общее решение уравнения имеет вид:
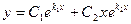
3) Если характеристическое уравнение имеет комплексные корни 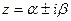 , то общее решение уравнения имеет вид:
, то общее решение уравнения имеет вид:
 .
.
Пример 1. Решить дифференциальное уравнение
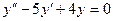 .
.
Решение. Составим характеристическое уравнение и решим его
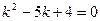 ;
;
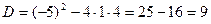 ;
;
 ;
; 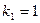 ;
; 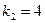 .
.
Тогда, 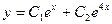 .
.
Пример 2. Решить дифференциальное уравнение
 .
.
Решение. Составим характеристическое уравнение и решим его
 ;
;
 ;
;
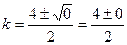 ;
; 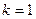 .
.
Тогда, 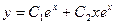 .
.
Пример 3. Решить дифференциальное уравнение
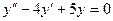 .
.
Решение. Составим характеристическое уравнение и решим его
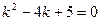 ;
;
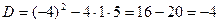 ;
;
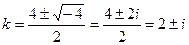 .
.
Тогда, 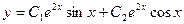 .
.
Неоднородные линейные дифференциальные уравнения второго порядка с постоянными коэффициентами
Пусть задано неоднородное линейное дифференциальное уравнение с постоянными коэффициентами:

Общее решение неоднородного дифференциального уравнения равно сумме общего решения соответствующего однородного уравнения и частного решения исходного однородного уравнения: 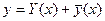 .
.
1) Пусть правая часть имеет вид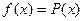 , где
, где 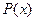 - многочлен от
- многочлен от 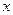 . Тогда частное решение уравнения будет иметь вид
. Тогда частное решение уравнения будет иметь вид  , где
, где  - многочлен той же степени, что и
- многочлен той же степени, что и 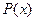 ;
; 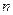 - количество корней характеристического уравнения, равных нулю.
- количество корней характеристического уравнения, равных нулю.
2) Пусть правая часть имеет вид , где
, где 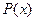 - многочлен от
- многочлен от 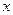 . Тогда частное решение уравнения будет иметь вид
. Тогда частное решение уравнения будет иметь вид 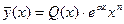 , где
, где  - многочлен той же степени, что и
- многочлен той же степени, что и 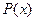 ;
; 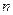 - количество корней характеристического уравнения, равных
- количество корней характеристического уравнения, равных  .
.
Пример. Решить дифференциальное уравнение
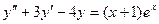 .
.
Решение. 1) Составим и решим соответствующее однородное уравнение:
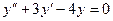 ;
;
Составим характеристическое уравнение и решим его
 ;
;
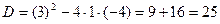 ;
;
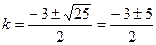 ;
; 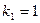 ;
;  .
.
Тогда,  .
.
2) Найдем частное решение исходного дифференциального уравнения в виде 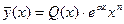 , где
, где  многочлен первой степени, а именно
многочлен первой степени, а именно 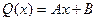 (коэффициенты
(коэффициенты 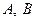 определяются методом неопределенных коэффициентов),
определяются методом неопределенных коэффициентов),  (так как однородное характеристическое уравнение имеет один корень, равный
(так как однородное характеристическое уравнение имеет один корень, равный 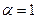 ).
).
Итак, 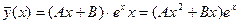 .
.
Тогда, 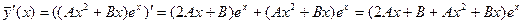 ;
;
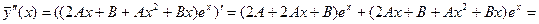

Таким образом,
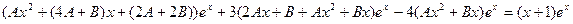 ;
;
 ;
;
 ;
;  .
.
Следовательно,  .
.
Общее решение исходного дифференциального уравнения прмет вид:
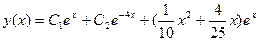 .
.