Знакоположительные ряды. Признаки сходимости
Пусть дана последовательность вещественных (действительных) чисел 
Числовым рядом называется бесконечная сумма членов числовой последовательности.
Краткая запись ряда: 
Числа  называются членами ряда, в частности
называются членами ряда, в частности 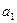 - первый член ряда,
- первый член ряда,  - n-ый или общий член ряда.
- n-ый или общий член ряда.
Ряд считается заданным, если известен общий член ряда  как функция его номера:
как функция его номера:  .
.
Введем суммы конечного числа членов ряда
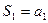 ,
,  ,…,
,…,  .
.
Сумма 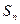 первых n членов ряда называется n-ой частичной суммой ряда. Ряд называется сходящимся, если существует конечный предел S последовательности его частичных сумм при неограниченном возрастании номера n, т.е.
первых n членов ряда называется n-ой частичной суммой ряда. Ряд называется сходящимся, если существует конечный предел S последовательности его частичных сумм при неограниченном возрастании номера n, т.е.
 .
.
Если конечный предел последовательности частичных сумм не существует, то ряд называется расходящимся.
Определение. Ряд
 ,
,
все члены которого положительны  , называется знакоположительным рядом.
, называется знакоположительным рядом.
Укажем сходимость некоторых числовых рядов, наиболее часто встречающихся на практике.
1. Геометрический ряд 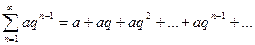
а) при  геометрический ряд расходится;
геометрический ряд расходится;
б) при  геометрический ряд сходится.
геометрический ряд сходится.
2. Гармонический ряд 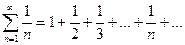 является расходящимся рядом.
является расходящимся рядом.
3. Обобщенный гармонический ряд (ряд Дирихле) - 
а) при 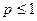 ряд расходится;
ряд расходится;
б) при  ряд сходится.
ряд сходится.
Теорема (необходимый признак сходимости).
Если ряд 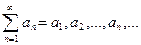 сходится, то его общий член стремится к нулю, т.е.
сходится, то его общий член стремится к нулю, т.е. 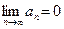 .
.
Достаточные признаки сходимости знакоположительных рядов
Теорема 1 (признак сравнения). Даны два знакоположительных рядов:
 (1)
(1)
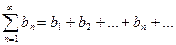 (2)
(2)
Пусть члены первого ряда не превосходят соответствующих членов второго ряда
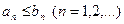 .
.
Тогда справедливы следующие утверждения:
1) если сходится ряд (2), то сходится и ряд (1);
2) если расходится ряд (1), то расходится и ряд (2).
Пример 1. Исследовать ряд на сходимость
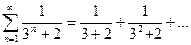
Решение. Рассмотрим геометрический ряд  . Он сходится, так как
. Он сходится, так как  . Сравним члены исходного ряда и геометрического ряда:
. Сравним члены исходного ряда и геометрического ряда:  . Следовательно, исходя из признака сравнения (пункт 1) данный ряд сходится.
. Следовательно, исходя из признака сравнения (пункт 1) данный ряд сходится.
Пример 2. Исследовать ряд на сходимость

Решение. Сравним данный ряд с гармоническим рядом 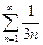 , который расходится:
, который расходится: 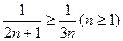 . Следовательно, согласно признаку сравнения (пункт 2), данный ряд расходится.
. Следовательно, согласно признаку сравнения (пункт 2), данный ряд расходится.
Теорема 2 (предельный признак сравнения). Предположим, что для рядов с положительными членами (1) и (2) выполняется предельное соотношение 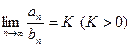 .
.
Тогда эти ряды ведут себя одинаково, т.е.:
1) если сходится ряд (1), то сходится и ряд (2);
2) если расходится ряд (1), то расходится и ряд (2).
Пример 3. Исследовать ряд на сходимость
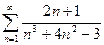 .
.
Решение. Рассмотрим ряд, сравнимый с данным рядом, сходимость которого известна. Так как нас интересует поведение членов ряда при 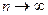 , то основную роль играют старшие члены в числителе и знаменателе. Поэтому сравним данный ряд с рядом, у которого общий член равен
, то основную роль играют старшие члены в числителе и знаменателе. Поэтому сравним данный ряд с рядом, у которого общий член равен  :
: 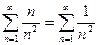 . Поскольку ряд
. Поскольку ряд 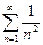 сходится (как обобщенный гармонический ряд), то в силу предельного признака сравнения данный ряд также сходится:
сходится (как обобщенный гармонический ряд), то в силу предельного признака сравнения данный ряд также сходится:
 .
.
Теорема 3 (признак Даламбера). Пусть для знакоположительного ряда (1) существует предел отношения последующего члена к предыдущему
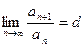 (возможно и бесконечность), тогда:
(возможно и бесконечность), тогда:
а) если  , то данный ряд сходится;
, то данный ряд сходится;
б) если  , то данный ряд расходится;
, то данный ряд расходится;
в) если 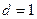 , то данный ряд не дает ответа на вопрос о сходимости ряда, требуется дополнительное исследование.
, то данный ряд не дает ответа на вопрос о сходимости ряда, требуется дополнительное исследование.
Пример 4. Исследовать ряд на сходимость
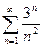
Решение. Имеем

 .
.
Следовательно, данный ряд расходится.
Теорема 4 (признак Коши). Пусть для знакоположительного ряда (1) существует предел 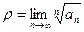 (может быть и бесконечность), тогда:
(может быть и бесконечность), тогда:
а) если 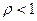 , то ряд (1) сходится;
, то ряд (1) сходится;
б) если 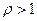 , то ряд (1) расходится;
, то ряд (1) расходится;
в) если 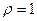 , то ничего определенного о поведении ряда сказать нельзя, нужно дополнительное исследование.
, то ничего определенного о поведении ряда сказать нельзя, нужно дополнительное исследование.
Пример 5. Исследовать ряд на сходимость
 .
.
Решение. Вычислим 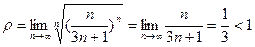 , следовательно, искомый ряд сходится.
, следовательно, искомый ряд сходится.
Теорема 5 (интегральный признак Коши-Маклорена). Пусть члены знакоположительного ряда (1) являются значениями при х=1, 2, …, n некоторой положительной, непрерывной и убывающей на промежутке [1, ∞) функции f(x):

Тогда
а) если сходится несобственный интеграл 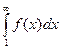 , то сходится и ряд (1);
, то сходится и ряд (1);
б) если 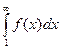 расходится, то ряд (1) расходится.
расходится, то ряд (1) расходится.
Пример. Исследовать ряд на сходимость
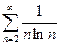 .
.
Решение. В нашем случае полагаем  для
для 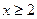 . Функция является положительной, непрерывной и убывающей на интервале [2, ∞).
. Функция является положительной, непрерывной и убывающей на интервале [2, ∞).
Далее отметим, что
 .
.
Таким образом, несобственный интеграл  расходится. Следовательно, по интегральному признаку данный ряд также расходится.
расходится. Следовательно, по интегральному признаку данный ряд также расходится.