Знакочередующиеся числовые ряды. Признак Лейбница
Определение. Числовой ряд, члены которого поочередно имеют то положительные, то отрицательные знаки, называется знакочередующемся рядом и записывается в виде
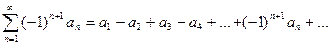 ,
,
где 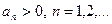 (ряд может начинаться и с отрицательного члена).
(ряд может начинаться и с отрицательного члена).
Теорема (признак Лейбница). Если члены знакочередующегося ряда монотонно убывают по абсолютной величине

и стремятся к нулю
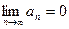 ,
,
то знакочередующийся ряд сходится, и сумма его не превосходит первого члена.
Пример. Исследовать на сходимость знакочередующийся ряд
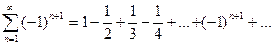
Решение. Сравним члены данного ряда по абсолютной величине
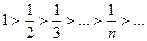
Видим, то члены искомого ряда монотонно убывают по абсолютной величине.
Найдем  .
.
Таким образом, согласно признаку Лейбница, искомый ряд сходится.
Сходимость произвольных рядов
Выясним вопрос о сходимости рядов
 ,
,
члены которых могут иметь произвольные знаки.
Теорема (достаточный признак сходимости числового ряда). Пусть дан ряд с членами произвольных знаков. Если сходится ряд
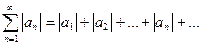 ,
,
составленный из абсолютных величин его членов, то сходится и данный ряд.
Пример. Исследовать сходимость ряда
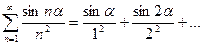
Решение. Данный ряд является произвольным. Рассмотрим ряд, составленный из абсолютных значений исходного ряда:
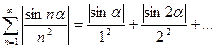 (*)
(*)
и ряд
 (**)
(**)
Члены ряда (*) не больше соответствующих членов ряда (**). Ряд (**) сходится, как обобщенный гармонический ряд, следовательно, сходится и ряд (*), а значит и исходный ряд.
Определение. Если числовой ряд сходится вместе с рядом, составленным из абсолютных величин его членов, то говорят, что числовой ряд сходится абсолютно.
Определение. Если числовой ряд сходится, а ряд, составленный из абсолютных величин его членов, то говорят, что числовой ряд сходится условно.
Пример. Определить, как сходится числовой ряд, абсолютно или условно?
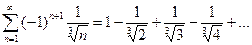
Решение. Исследуем исходный ряд на сходимость.
Так как 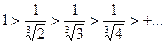 , следовательно, видим, что члены ряда убывают по абсолютной величине. Кроме того,
, следовательно, видим, что члены ряда убывают по абсолютной величине. Кроме того, 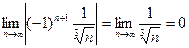 .
.
Таким образом, согласно признаку Лейбница, искомый ряд сходится.
Рассмотрим ряд, составленный из абсолютных величин данного ряда:
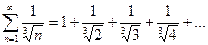
Этот ряд расходится как обобщенный гармонический ряд ( ). Делаем вывод, что данный ряд сходится условно.
). Делаем вывод, что данный ряд сходится условно.