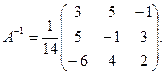Определители
Важной характеристикой квадратной матрицы А порядка n является ее определитель
1. Рассмотрим это понятие для матриц второго порядка.
Пусть задана матрица
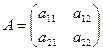 .
.
Определитель матрицы А – число которое ставится в соответствие матрице А и вычисляется по правилу det A= 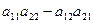 .
.
Обозначение: det A= =
= 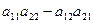 .
.
Например, det A=
2. Рассмотрим квадратную матрицу третьего порядка.
Определитель третьего порядка это число
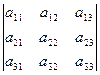 =
= .
.
Например,  =
=
=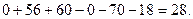
3. Определители n-го порядка.
Минор  элемента
элемента 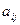 матрицы
матрицы  - это определитель порядка n-1, полученный из матрицы А вычеркиванием i-той строки и j-ого столбца, на пересечении которых стоит этот элемент.
- это определитель порядка n-1, полученный из матрицы А вычеркиванием i-той строки и j-ого столбца, на пересечении которых стоит этот элемент.
Алгебраическое дополнение 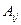 отличается от минора лишь знаком:
отличается от минора лишь знаком:
 .
.
Определителем матрицы А n-го порядка называется число, полученное разложением по i-й строке:
 .
.
Пример. Вычислить определитель матрицы 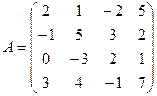
Вычислим определитель матрицы разложением его по элементам третьей строки (так как эта строка содержит нулевой элемент):
det A=0·А31+(-3)·А32+2·А33+1·А34=-3·А32+2·А33+А34
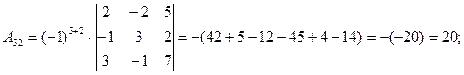


Тогда, det A=-3·20+2·(-28)-12=-60-56-12=-128.
Основные свойства определителей
1. При умножении всех элементов некоторой строки на число определитель исходной матрицы умножается на это число.
2. Определитель матрицы с нулевой строкой равен нулю
3. При перестановке двух строк определитель меняет знак.
4. Если две строки матрицы равны, то ее определитель равен нулю.
5. Определитель не меняется, если к какой-нибудь строке матрицы прибавить другую ее строку, умноженную на число.
6. Определитель произведения двух матриц равен произведению определителей: 
7. Определитель не меняется при транспонировании матрицы.
Замечание 1. При элементарных преобразования Гаусса определитель матрицы может только изменить знак (при перестановке строк). Поэтому удобно считать определитель матрицы, предварительно приведя ее к ступенчатому виду.
Замечание 2. Преобразование Гаусса сводит квадратичную матрицу к верхнетреугольному виду, определитель которой равен произведению диагональных элементов.
Замечание 3. Если ранг матрицы равен ее порядку, то строки матрицы линейно независимы. Таким образом, равенство нулю определителя есть признак линейной зависимости строк матрицы.
Обратная матрица
Матрица А-1 называется обратной к матрице А, если выполняется условие А· А-1= А-1·А=Е.
Теорема. Матрица А имеет обратную А-1 тогда и только тогда, когда А – невырожденная, det A≠0.
Способы вычисления обратной матрицы
1. Способ вычисления обратной матрицы с помощью алгебраических дополнений.
Алгоритм вычисления:
1) вычисляют определитель матрицы det A;
2) для каждого элемента 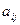 вычисляют алгебраические дополнения
вычисляют алгебраические дополнения 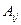 ;
;
3) составляют матрицу  из алгебраических дополнений:
из алгебраических дополнений:
 ;
;
4) транспонируют матрицу  :
:
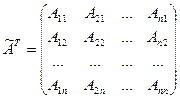
Матрица  называется присоединенной к матрице А;
называется присоединенной к матрице А;
5) определяют обратную матрицу по формуле:
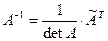 .
.
Пример. Найти матрицу, обратную к матрице 
1) det A=0+20-6-0+20+8=42
2) 
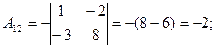

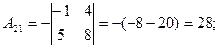
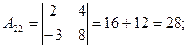
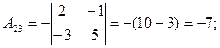
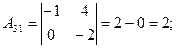


3) 
4) 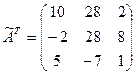 ;
;
5) 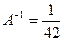
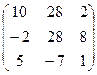 .
.
Сделаем проверку, убедимся, что полученная матрица искомая:
А· А-1=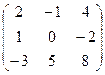

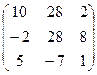 =
=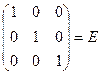 .
.
2. Метод Гаусса вычисления обратной матрицы.
1) припишем к матрице А единичную матрицу того же порядка:
 .
.
С помощью элементарных преобразований приведем матрицу  сначала к ступенчатому виду, добьемся того, чтобы слева оказалась единичная матрица Е, тогда справа окажется обратная матрица
сначала к ступенчатому виду, добьемся того, чтобы слева оказалась единичная матрица Е, тогда справа окажется обратная матрица  .
.
Пример. 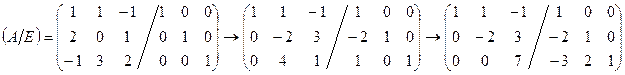

 Итак,
Итак,