Системы линейных уравнений
Рассмотрим систему m уравнений с n неизвестными
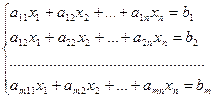 (1)
(1)
Матрица А, составленная из коэффициентов при неизвестных системы, называется матрицей системы уравнений (1):
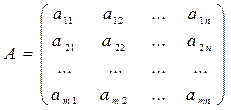
Матрица  называется расширенной матрицей.
называется расширенной матрицей.
Вектор 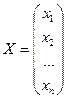 называется вектором неизвестных, вектор
называется вектором неизвестных, вектор 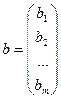 называется вектором свободных членов.
называется вектором свободных членов.
Матричная запись системы (1) имеет вид:

Если вектор b=0, то система называется однородной, если b≠0 (хотя бы один из элементов отличен от нуля), то система называется неоднородной.
Решением системы (1) называется такой вектор X=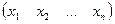 , что при подстановке чисел
, что при подстановке чисел  в систему (1) получаются верные равенства (тождества).
в систему (1) получаются верные равенства (тождества).
Система, имеющая хотя бы одно решение, называется совместной, в противном случае – несовместной.
Две системы называются эквивалентными, если множества их решений совпадают. Заметим, что операции над системой уравнений сводятся к элементарным преобразованиям над расширенной матрицей 
Однородные системы
Рассмотрим однородную систему 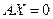 .
.
Заметим, что однородная система всегда совместна, поскольку нуль-вектор Х=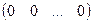 ее решение.
ее решение.
Для решения однородной системы уравнений применяется метод Гаусса. Метод Гаусса для решения систем уравнений состоит из прямого и обратного хода. Прямым ходом заданную систему приводят к эквивалентной ступенчатой системе.
Проиллюстрируем алгоритм метода на примере:

Прямой ход метода Гаусса. Приведем матрицы системы к ступенчатому виду:
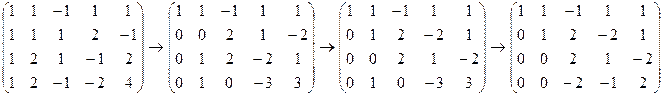
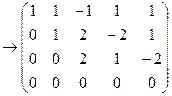 .
.
Матрица приведена к ступенчатому виду, ее ранг равен 3.
Выпишем соответствующую систему уравнений:
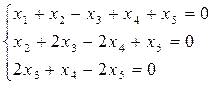
Переменные 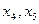 , не связанные с угловыми элементами, называются свободными, переменные
, не связанные с угловыми элементами, называются свободными, переменные 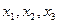 - зависимые переменные (несвободные, базисные). Зависимыми переменными всегда объявляются переменные, коэффициентами которых являются угловые элементы. Заметим, что при другом способе приведения матрицы к ступенчатому виду свободными переменными могут оказаться переменные с другими индексами. Однако число свободных переменных всегда равно n-r (r – ранг матрицы).
- зависимые переменные (несвободные, базисные). Зависимыми переменными всегда объявляются переменные, коэффициентами которых являются угловые элементы. Заметим, что при другом способе приведения матрицы к ступенчатому виду свободными переменными могут оказаться переменные с другими индексами. Однако число свободных переменных всегда равно n-r (r – ранг матрицы).
Обратный ход метода Гаусса заключается в том, что зависимые переменные выражаются через свободные из ступенчатой системы, начиная с последнего уравнения и «поднимаясь» вверх к первому. В результате получим
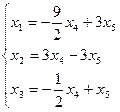
Полученное выражение называют общим решением системы в координатной форме.
Полученные выражения дают описание всего множества решений однородной системы. Давая свободным переменным произвольные значения, и вычисляя значения зависимых переменных, получаем некоторое частное решение системы.
Запишем общее решение в векторной форме. Придадим свободным переменным значения  , получим
, получим 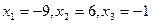 и
и 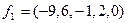 ; затем
; затем 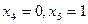 , получим
, получим  и
и 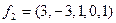 . Векторы
. Векторы 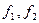 линейно независимы и образуют фундаментальную систему решений (ФСР).
линейно независимы и образуют фундаментальную систему решений (ФСР).
Общее решение системы, записанное в векторной форме, имеет вид:
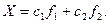

Неоднородные системы
Пусть задана неоднородная система уравнений
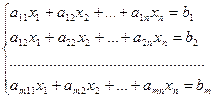
Теорема Кронекера-Капелли (критерий совместности неоднородной системы). Система совместна тогда и только тогда, когда ранг основной матрицы А равен рангу расширенной матрицы  :
: 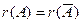 .
.
Методы решения систем линейных уравнений
1. Метод Гаусса
Рассмотрим на примере системы 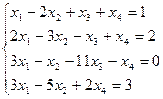
Прямой ход метода Гаусса. Приведем расширенную матрицу системы к ступенчатому виду:
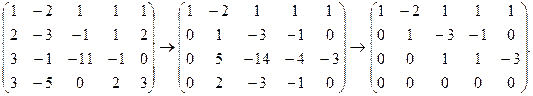
Здесь  , система совместна.
, система совместна.
Запишем эквивалентную ступенчатую систему:
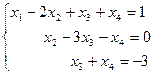
Переменные 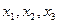 являются зависимыми, а
являются зависимыми, а 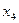 - свободной переменной.
- свободной переменной.
Обратный ход метода Гаусса. Выразим зависимые переменные через свободные, получим:
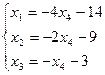 .
.
Пример 2. Решить систему уравнений методом Гаусса
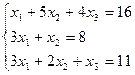 .
.
Составим расширенную матрицу и приведем ее к ступенчатому виду:
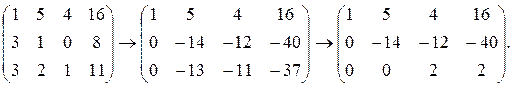
Запишем эквивалентную ступенчатую систему:
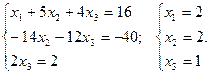
Таким образом, решением данной системы уравнений является вектор  .
.
2. Метод решения системы уравнений с помощью обратной матрицы.
Найдем решение системы уравнений из примера 2 с помощью обратной матрицы. Прежде всего, определим обратную матрицу А-1 с помощью алгебраических дополнений.
det A=
Для каждого элемента определим алгебраические дополнения:
 ,
, 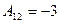 ,
,  ,
,  ,
, 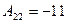 ,
, ,
,  ,
,  ,
, 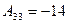 .
.
Тогда, А-1 = .
.
Решение системы уравнений имеет вид:
Х=
 .
.
Таким образом, решением данной системы уравнений является вектор  .
.
3. Метод Крамера решения системы уравнений.
Рассмотрим неоднородную систему уравнений 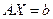 с невырожденной матрицей А (det A≠0):
с невырожденной матрицей А (det A≠0):
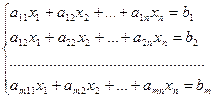
Теорема Крамера. Система 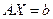 , где det A≠0, имеет единственное решение, которое вычисляется по формулам:
, где det A≠0, имеет единственное решение, которое вычисляется по формулам:
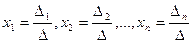 ,
,
где Δ= det A, 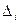 - получается из определителя Δ заменой i-го столбца на столбец свободных членов.
- получается из определителя Δ заменой i-го столбца на столбец свободных членов.
Пример. Найти решение системы уравнений методом Крамера
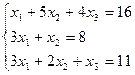 .
.
Решение.
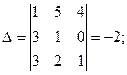
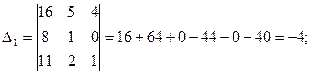
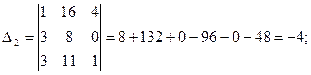
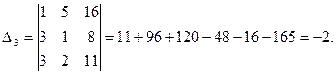
Итак, 