Дано координати точок: А (–1; 4; 2); В(0; 3; 3); С(4; –5; 3) і М(1; –3; 5).

Потрібно: 1) скласти рівняння площини Q, що проходить через точки А, В, С; 2) скласти канонічні рівняння прямої, що проходить через точку М перпендикулярно площині Q; 3) знайти точки перетину отриманої прямої з площиною Q та з координатними площинами х0у, х0z, y0z.

►1) Рівняння площини, що проходить через 3 точки А(х₁; у₁; z₁), В(х₂; у₂; z₂) і С(х₃; у₃; z₃).

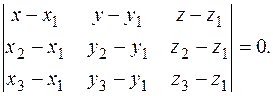(11.11)

 

Підставляючи координати точок А, В, С в (11.11), маємо

 

,

 

або, розкладаючи визначник за елементами першого рядка, маємо

(x + 1)8 + ( y – 4)4 + ( z – 2)( –4) = 0,

2(x + 1) + y – 4 – z + 2 + 0;

2x + y – z = 0 – рівняння площини Q.

2) Пряма в просторі задається канонічними рівняннями

(11.12)

де а, в, с – координати точки, через яку проходить пряма, а m, n, p – координати напрямного вектора цієї прямої.

Умови перпендикулярності прямої (11.12) до площини Ax + By + + Cz + D = 0 мають вигляд:

Запишемо умови перпендикулярності шуканої прямої до площи-ни Q:

Цим умовам, зокрема, задовольняють наступні координати: m = 2; n = 1; p = –1.

Отже рівняння шуканої прямої:

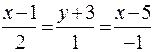. (11.13).

3) Запишемо рівняння прямої (11.13) у параметричному вигляді. Нехай

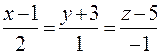= t,

де t - деякий параметр. Тоді

х = 2t + 1; y=t – 3; z = – t + 5. (11.14)

Підставивши (11.14) в рівняння площини Q, маємо

2(2t + 1) + (t – 3) – (–t + 5) = 0; 6t – 6 = 0; t = 1.

Покладаючи в (11.14) t = 1, знаходимо координати точки Р перетину прямої (11.13) з площиною Q. Отже, P (3; –2; 4).

Нехай Р₁ – точка перетину прямої (11.13) з координатною площиною х0у.

Очевидно, що в цьому разі z = 0. Тоді, покладаючи в (11.14) z = 0, маємо t = 5; x = 11, y = 2. Отже, Р₁ (11, 2, 0) – точка перетину прямої (11.14) з площиною x0y.

Аналогічно знаходимо P₂(7; 0; 2) – точку перетину прямої (11.13) з площиною х0z; P₃– точка перетину з площиною у0z.