Розв’язання типового варіанта.
1.Знайти границі:
a) 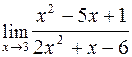 ; b)
; b) 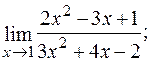
в)  г)
г) 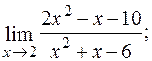
д) 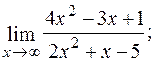 е)
е) 
► а) Під знаком границі маємо дробово-раціональну функцію, знаменник якої при х = 3 (граничне значення аргументу) відмінний від нуля. Користуючись теоремою про границю частки і замінюючи аргумент х його граничним значенням, маємо
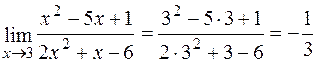 .
.
б) При х=1 знаменник дробу відмінний від нуля, чисельник дорівнює нулю. Отже, при  чисельник є величиною нескінченно малою, а знаменник – змінна величина, що має кінцеву границю. Оскільки частка від ділення нескінченно малої величини на змінну величину, що має кінцеву границю, є також нескінченно малою величиною, то границею даного дробу є нуль.
чисельник є величиною нескінченно малою, а знаменник – змінна величина, що має кінцеву границю. Оскільки частка від ділення нескінченно малої величини на змінну величину, що має кінцеву границю, є також нескінченно малою величиною, то границею даного дробу є нуль.
Отже,
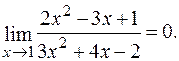
в) При х = – 2 знаменник дробу дорівнює нулю, а чисельник від-мінний від нуля. Отже, при 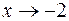 знаменник є величина не скін-ченно мала, а чисельник – обмежена. Дана дріб є нескінченно вели-кою, умовно це позначається символом ¥. Таким чином,
знаменник є величина не скін-ченно мала, а чисельник – обмежена. Дана дріб є нескінченно вели-кою, умовно це позначається символом ¥. Таким чином,
 .
.
г) При х=2 чисельник і знаменник дробу дорівнюють нулю. Отже, безпосередня підстановка граничного значення аргументу призводить до невизначеного виразу виду  . Щоб розкрити невизначеність виду
. Щоб розкрити невизначеність виду  (відношення двох нескінченно малих величин), необхідно попередньо дріб спростити, розклавши на множники чисельник і знаменник та скоротивши дріб на (х – 2):
(відношення двох нескінченно малих величин), необхідно попередньо дріб спростити, розклавши на множники чисельник і знаменник та скоротивши дріб на (х – 2):
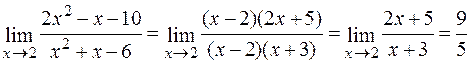 .
.
Слід відмітити, що аргумент х прямує до свого граничного значення 2, але не співпадає з ним. З цього приводу множник (х – 2) є відмінним від нуля при x® 2.
д) При х® ¥ маємо невизначений вираз виду  . Щоб знайти
. Щоб знайти
границю дробово-раціональної функції 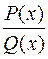 при
при 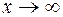 , необхідно попередньо чисельник і знаменник даного дробу поділити на
, необхідно попередньо чисельник і знаменник даного дробу поділити на 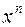 , де n – найвищий ступінь багаточленів Р(х) та Q(х). Поділивши чисельник і знаменник даного дробу на x2, застосовуючи основні теореми про границі та властивості нескінченно малих, маємо
, де n – найвищий ступінь багаточленів Р(х) та Q(х). Поділивши чисельник і знаменник даного дробу на x2, застосовуючи основні теореми про границі та властивості нескінченно малих, маємо
 .
.
е) Безпосередня підстановка граничного значення аргументу призводить до невизначеності виду  . Щоб розкрити цю невизна-ченість, помножимо чисельник та знаменник дробу на добуток
. Щоб розкрити цю невизна-ченість, помножимо чисельник та знаменник дробу на добуток 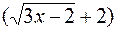 (
(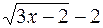 ).
).
Потім скоротимо дріб на множник (х – 2), що є відмінним від нуля при 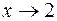 .
.
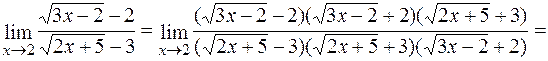

=  .◄
.◄
2.Знайти границі:
a) 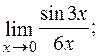 б)
б) 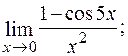 в)
в) 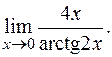
►а) Першою визначною границею зветься границя відношення синуса нескінченно малої дуги до самої дуги. Відомо, що ця границя дорівнює одиниці, тобто  .
.
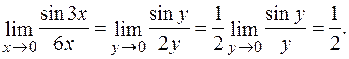 |
Нехай 3х = у. Очевидно, що при
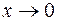 і
і  . Тоді
. Тоді
б) Відомо, що 1 – сos5x = 2sin2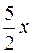 . Отже,
. Отже,
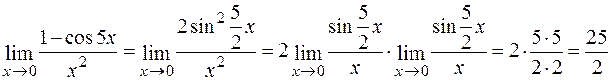 .
.
в) Позначимо arctg2x = y, тоді 2x = tgy, очевидно, що при 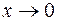 і
і  ; використовуючи теореми про границі, маємо:
; використовуючи теореми про границі, маємо:
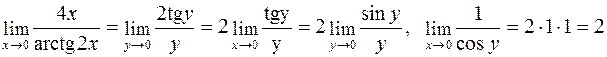 .◄
.◄