Розв’язання типового варіанта
1.Знайти похідні функцій:
а)y=ln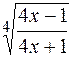 ; б) y=
; б) y=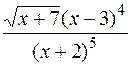 ; в) y=(tg2x)lnx ;
; в) y=(tg2x)lnx ;
г) 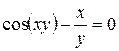 ; д)
; д) 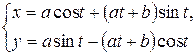 .
.
► а) y=ln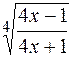 .
.
Користуючись властивостями логарифмів, перетворимо праву частину:
y=ln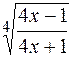 =
=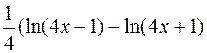 .
.
Застосовуючи правила диференціювання, маємо:
y'= 
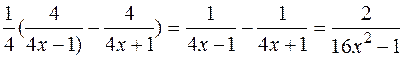 .
.
б) y= 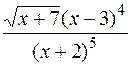 .
.
Прологарифмуємо дану функцію, застосовуючи властивості логарифмів:
lny= 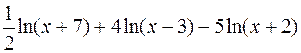 .
.
Продиференціюємо по х обидві частини отриманої рівності, вважаючи 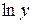 складеною функцією від змінної х.
складеною функцією від змінної х.
(lny)′ = 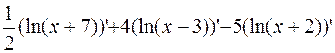 .
.
Або
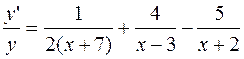 ;
;
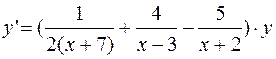 ;
;
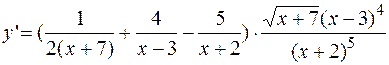 .
.
в) y=(tg2x)lnх.
Прологарифмуємо функцію:
lny=lnx×lntg2x.
Знайдемо похідну від лівої і правої частини останньої рівності по х.
(lny)′=(lnx)′×lntg2x+lnx(lntg2x)′ .
Звідки
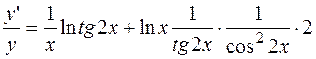 .
.
Далі
y′=y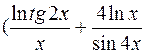 ).
).
Остаточно маємо:
y′=(tg2x)lnx 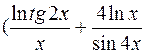 ).
).
г) 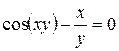 .
.
У даному випадку залежність між аргументом х та функцією у задана рівнянням, яке не розв’язане відносно функції у. Щоб знайти похідну 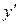 , необхідно продиференціювати по х обидві частини заданого рівняння, вважаючи при цьому змінну у функцією від х, і потім отримане рівняння розв’язати відносно шуканої похідної
, необхідно продиференціювати по х обидві частини заданого рівняння, вважаючи при цьому змінну у функцією від х, і потім отримане рівняння розв’язати відносно шуканої похідної 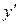 .
.
Маємо: 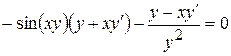 .
.
З отриманої рівності, що зв’язує х, у та 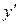 , знаходимо похідну
, знаходимо похідну 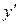 :
:
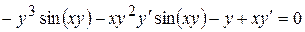 ,
,
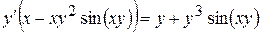 ,
,
Звідки
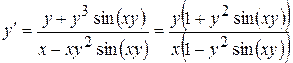 .
.
д) 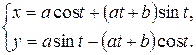
Залежність між змінними х та у задано параметричними рівняннями. Щоб знайти шукану похідну 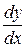 , знаходимо попередні диференціали
, знаходимо попередні диференціали 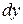 і
і 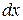 і потім знаходимо відношення цих диференціалів
і потім знаходимо відношення цих диференціалів
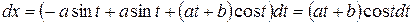 ,
,
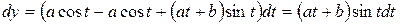 ,
,
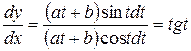 . ◄
. ◄
2.За допомогою диференціала обчислити наближене значення  .
.
► Розглянемо функцію 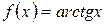 . Покладемо
. Покладемо 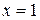 ,
, 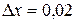 і застосуємо формулу
і застосуємо формулу
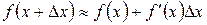 .
.
У нашому випадку 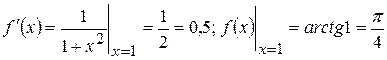 .
.
Отже, маємо
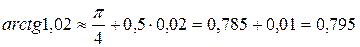 . ◄
. ◄
3.Дослідити функцію y = x4 - 8x2 + 16 методами диференційного числення та побудувати її графік.
►Дослідження функції та побудову графіка можна здійснити за наступною схемою:
1) знайти область визначення функції;
2) дослідити функцію на парність або непарність;
3) знайти точки перетину графіка функції з осями координат;
4) дослідити функцію на неперервність, знайти точки роз-риву;
5) знайти асимптоти графіка функції;
6) знайти інтервали монотонності та точки екстремуму;
7) знайти інтервали опуклості, угнутості та точки перегину;
8) побудувати графік функції, користуючись результатами дослідження.
1.Дана функція є многочленом, тому вона визначена (існує) та неперервна на всій дійсній вісі.
2. Дана функція є парною, тому що
у(-x) = ( -x)4 - 8(-x)2 + 16 = x4 - 8x + 16 = у(x).
Отже, графік цієї функції є симетричним відносно осі ординат.
3. Точки перетину графіка функції з віссю ОY визначаємо підстановкою у функцію значення х = 0, що дає (0;16); точки перети-ну графіка з віссю ОX знаходимо, прийнявши у=0, з рівняння x4-8x2+16=0, корені якого x1,2 =-2 та x3,4 =2 є абсцисами точок (-2;0) та (2, 0). Але в цих точках графік не перетинає, а лише торкається осі ОX, тому що кожне з чисел –2 і 2 є подвійним коренем даної функції, в чому легко переконатись, записавши її у вигляді: y = (x+2)2 (x-2)2.
4. Фукція є непервною.
5. Графік функції вертикальних та похилих асимптот не має.
6. Знайдемо інтервали монотонності функції та точки екстремуму. Перша похідна:
y′ = 4x3-16 x = 4x(x2-4) = 4x(x-2)(x+2)
дорівнює нулю при x1 = -2; x2 = 0; x3 = 2.
Розіб’ємо всю числову вісь на чотири інтервали:
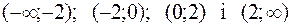 .
.
Склавши таблицю, визначимо знак похідної на кожному з цих інтервалів та характер поведінки функції.
| x | 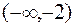
| -2 | -2,0) | (0,2) | (2,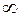 ) )
| ||
| y′ | - | + | - | + | |||
| y | спадає | min | зростає | max | спадає | min | зростає |
Отже, при x = -2 та x = 2 функція має мінімум, а при x = 0 – максимум, причому
у(-2) = у(2) = 0; у(0) = 16.
5. Знайдемо інтервали опуклості, угнутості та точки перегину графіка функції. Друга похідна
y′′=(4x3-16x)′=12x2-16=12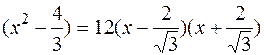 .
.
Вона має два корені, які поділяють числову вісь на проміжки:
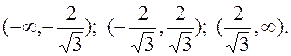
Складемо таблицю, визначивши знак другої похідної на кожному з цих проміжків, знайдемо інтервали опуклості, угнутості та точки перегину.
| x | 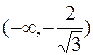
| 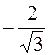
| 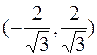
| 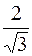
| 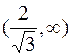
|
| y′′ | + | - | + | ||
| y | угнута | перегин | опукла | перегин | угнута |
Отже, при 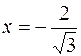 та при
та при 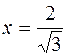 маємо точки перегину, причому
маємо точки перегину, причому
у(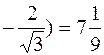 ; у
; у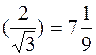 .
.
На основі отриманих даних будуємо графік функції y (рис. 4).
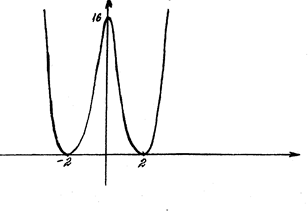
Рис. 4 ◄
4.Дослідити функцію 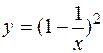 методами диференційного числення та побудувати її графік.
методами диференційного числення та побудувати її графік.
►1. Задана функція існує при всіх значеннях аргументу, крім х=0. Область визначення складається з двох інтервалів (-¥ , 0) та (0 , ¥).
2. Функція не є парною або непарною.
3. З віссю ОУ графік функції не перетинається. Точки перетину графіка функції з віссю ОХ:
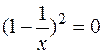 ; х = 1.
; х = 1.
Відзначимо, що y ³ 0 для всіх значень x.
4. Функція має нескінченний розрив при х = 0, причому
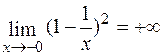 ;
; 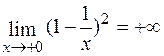 .
.
При всіх інших значеннях аргументу дана функція неперервна.
5. Оскільки х=0 – точка розриву (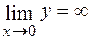 ), то х=0 – рівняння вертикальної асимптоти. Для визначення рівняння похилої асимптоти y = kx + b скористуємося відомими формулами
), то х=0 – рівняння вертикальної асимптоти. Для визначення рівняння похилої асимптоти y = kx + b скористуємося відомими формулами
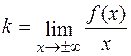 i
i 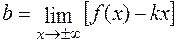 .
.
Маємо
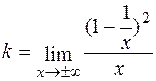 =0;
=0; 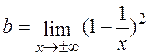 =1.
=1.
Отже, пряма y=1 є горизонтальною асимптотою графіка функції.
6. Знайдемо інтервали монотонності та точки екстремуму функції.
Перша похідна
y′= 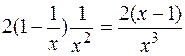 .
.
Неважко бачити, що перша похідна дорівнює нулю при х=1 і обертається в нескінченність при х=0. Але при х=0 функція невизначена, отже ця точка не підлягає дослідженню. Розіб’ємо всю числову вісь на три інтервали: 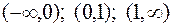 . Склавши таблицю, визначимо знак похідної на кожному з цих інтервалів та точки екстремуму.
. Склавши таблицю, визначимо знак похідної на кожному з цих інтервалів та точки екстремуму.
| x | (-¥ , 0) | (0,1) | 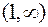
| ||
| y′ | + | не існує | - | + | |
| y | зростає | не існує | спадає | min | зростає |
Отже, при x = 1 функція має мінімум, ymin= 0.
7. Знайдемо інтервали опуклості, угнутості та точки перегину графіка функції. Друга похідна
y′′=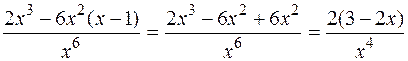 .
.
З одержаного виразу видно, що друга похідна дорівнює нулю при x=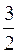 і обертається в нескінченність при x=0. Оскільки при x=0 функція не існує, то ця точка не підлягає дослідженню. Розіб’ємо область існування функції на інтервали:
і обертається в нескінченність при x=0. Оскільки при x=0 функція не існує, то ця точка не підлягає дослідженню. Розіб’ємо область існування функції на інтервали: 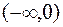 ; (0,
; (0, 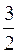 ); (
); (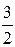 ,
,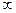 ).
).
Склавши таблицю, визначимо знак другої похідної на кожному з цих інтервалів та точки перегину.
| x | (-¥ , 0) | (0,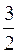 ) )
| 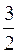
| (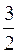 , ,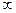 ) )
| |
| y′′ | + | не існує | + | - | |
| y | угнута | не існує | угнута | перегин | опукла |
Отже, при x= 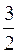 маємо точку перегину:
маємо точку перегину:
y(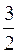 )=(1-
)=(1-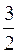 )2=
)2=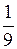 .
.
Таким чином, P(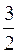 ,
, 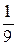 ) - точка перегину.
) - точка перегину.
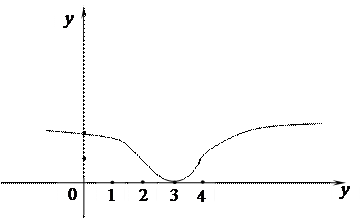
8. На основі отриманих даних будуємо графік функції (Рис. 5).
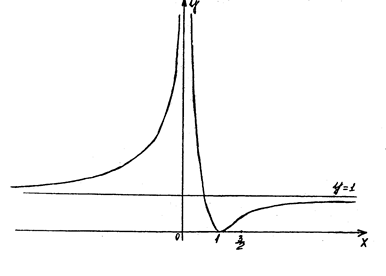
(Рис. 5) ◄
5. Дослідити функцію 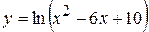 методами диференціального числення та побудувати її графік.
методами диференціального числення та побудувати її графік.
► 1) Область визначення функції 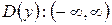 , тому що квадратний тричлен, що знаходиться під знаком логарифма завжди приймає додатні значення, тобто:
, тому що квадратний тричлен, що знаходиться під знаком логарифма завжди приймає додатні значення, тобто:
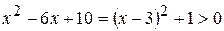 .
.
2) Функція не є парною або непарною, тому що
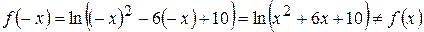 .
.
3) Точки перетину графіка функції з осями координат: 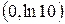 ;
; 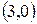 .
.
4) Функція є неперервною.
5) Вертикальних асимптот графік функції не має. Рівняння похилих асимптот шукаємо у вигляді 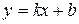 , де
, де
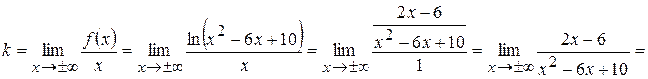
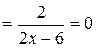 .
.
Відмітимо, що при знаходженні границі двічі було застосовано правило Лопіталя.
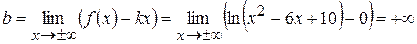 .
.
Отже, графік функції асимптот не має.
6) Визначимо інтервали монотонності та точки екстремуму. Знаходимо першу похідну
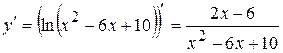 .
.
Для знаходження критичних точок першого роду розв’яжемо рівняння 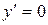 , тобто
, тобто 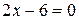 ,
, 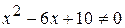 , звідки
, звідки 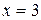 - критична точка першого роду.
- критична точка першого роду.
Критична точка 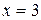 поділяє область визначення функції на два інтервали
поділяє область визначення функції на два інтервали 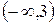 і
і 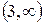 . Очевидно, що
. Очевидно, що
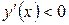 при
при 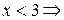 функція спадає;
функція спадає;
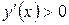 при
при 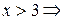 функція зростає;
функція зростає;
 при
при 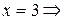 функція має екстремум (мінімум);
функція має екстремум (мінімум); 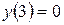 .
.
7) Визначимо інтервали опуклості, угнутості, точки перетину.
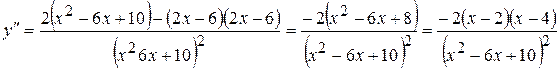 .
.
Для знаходження критичних точок другого роду розв’яжемо рівняння 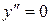 , тобто
, тобто 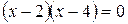 ,
, 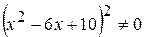 , звідки
, звідки 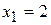 ,
, 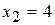 - критичні точки другого роду, які поділяють область визначення функції на інтервалі, що вказані у наведеній нижче таблиці.
- критичні точки другого роду, які поділяють область визначення функції на інтервалі, що вказані у наведеній нижче таблиці.
| х | 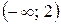
| (2; 4) | (4; ¥) | ||
Знак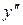
| - | + | - | ||
| Поведінка графіка функції | опуклий

| перегин | угнутий

| перегин | опуклий
|
Отже, графік функції має дві точки перегину 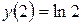 ,
, 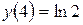 .
.
На основі дослідження поступово будуємо графік функції 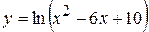 , який наведено на рисунку
, який наведено на рисунку