Завдання 14.
В задачах варіантів 1 - 25 знайти частинні похідні та повний диференціал функції z = z(x, y).
1. 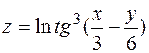 . 2.
. 2. 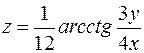 .
.
3. 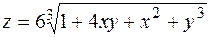 . 4.
. 4.  .
.
5.  . 6.
. 6. 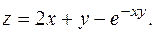
7. 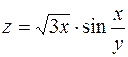 . 8.
. 8.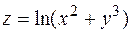 .
.
9. 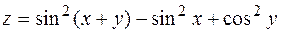 . 10.
. 10. 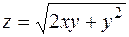 .
.
11. 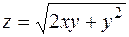 . 12.
. 12. 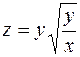 .
.
13.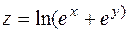 . 14.
. 14. 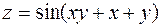 .
.
15. 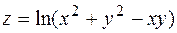 . 16.
. 16. 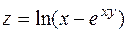 .
.
17. 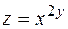 . 18.
. 18. 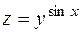 .
.
19. 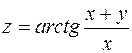 . 20.
. 20. 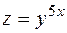 .
.
21. 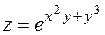 . 22.
. 22. 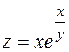 .
.
23. 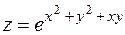 . 24.
. 24.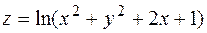 .
.
25. 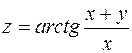 .
.
Завдання 15. В задачах варіантів 1-25 обчислити за допомогою повного диференціала наближене значення заданої величини.
1.  . 2.
. 2. 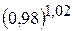 . 3.
. 3. 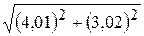 .
.
4. 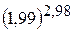 . 5.
. 5. 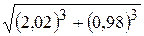 . 6.
. 6. 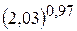 .
.
7. 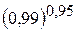 . 8.
. 8. 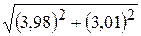 . 9.
. 9. 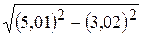 .
.
10. 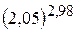 . 11.
. 11. 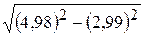 . 12.
. 12. 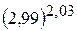 .
.
13. 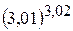 . 14.
. 14. 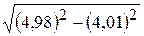 . 15.
. 15. 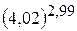 .
.
16. 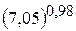 . 17.
. 17. 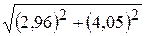 . 18.
. 18. 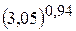 .
.
19.  . 20.
. 20. 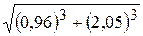 . 21.
. 21. 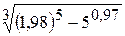 .
.
22. 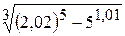 . 23.
. 23. 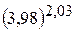 . 24.
. 24. 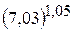 .
.
25. 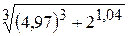 .
.
Завдання 16. В задачах варіантів 1-25 задану функцію 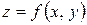 дослідити на екстремум.
дослідити на екстремум.
1. 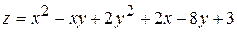 . 2.
. 2. 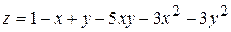 .
.
3. 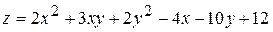 . 4.
. 4. 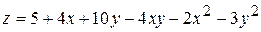 .
.
5. 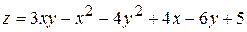 . 6.
. 6. 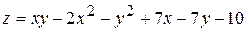 .
.
7. 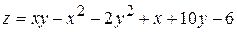 . 8.
. 8. 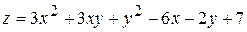 .
.
9. 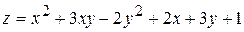 . 10.
. 10. 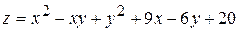 .
.
11. 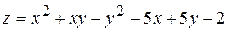 . 12.
. 12. 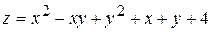 .
.
13. 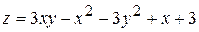 . 14.
. 14. 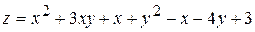 .
.
15. 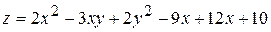 . 16.
. 16. 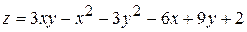 .
.
17. 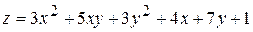 . 18.
. 18. 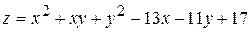 .
.
19. 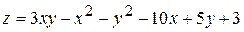 . 20.
. 20. 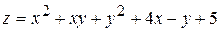 .
.
21. 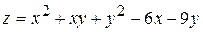 . 22.
. 22. 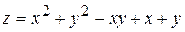 .
.
23. 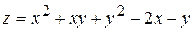 . 24.
. 24. 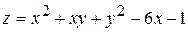 .
.
25. 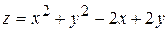 .
.
Розв’язання типового варіанта.
1.Знайти частинні похідні та повний диференціал функції
z = arctg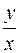 .
.
► Частинна похідна функції z = z(x,y) по x визначається за правилами диференціювання функції однієї змінної, причому інші змінні вважаються постійними; аналогічно визначається частинна похідна по у, де всі змінні, крім у, вважаються постійними.
Отже,

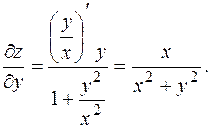
Повний диференціал даної функції визначається за формулою
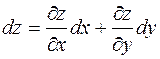 .
.
Отже, маємо:
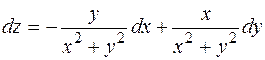 .◄
.◄
2.За допомогою повного диференціала обчислити наближено 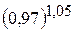 .
.
► Розглянемо функцію 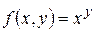 і застосуємо формулу
і застосуємо формулу
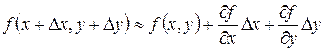 ,
,
Поклавши 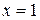 ,
,  ,
, 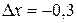 ;
; 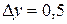 .
.
Врахуємо, що 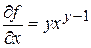 ;
; 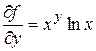 ;
;
 ;
; 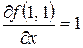 ;
; 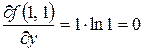 .
.
Отже, 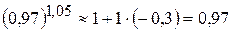 . ◄
. ◄
3. Дослідити на екстремум функцію 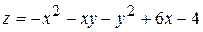 .
.
► Знаходимо частинні похідні першого порядку функції 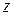
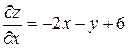 ;
; 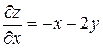 .
.
Для визначення стаціонарних точок згідно з необхідними умовами екстремуму, прирівнюємо до нуля ці похідні. Маємо таку систему рівнянь:
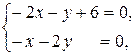
розв’язок якої  ,
, 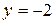 .
.
Отже, дана функція має тільки одну стаціонарну точку 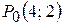 .
.
Для перевірки достатніх умов екстремуму знаходимо частинні похідні другого порядку
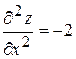 ;
; 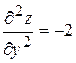 ;
; 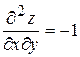 .
.
Як видно, частинні похідні другого порядку мають постійні значення в будь-якій точці, зокрема в точці 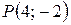 .
.
Обчислимо 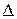 для точки
для точки 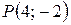 , де
, де 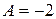 ;
;  ;
; 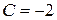 .
.
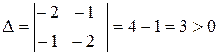 .
.
Тому що 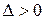 та
та 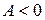 , то в точці
, то в точці 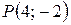 задана функція має максимум.
задана функція має максимум.
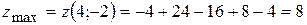 .◄
.◄