Дане рівняння приймає вигляд

2xxtdx+(x²t²-x²)(tdx+xdt)=0.

Скоротивши на х² , маємо:

2tdx+(t²-1) (tdx+xdt)=0;

2tdx+(t²-1) tdx+x(t²-1)dt=0;

t(2+t²-1)dx+x(t²-1)dt=0;

t(1+t²)dx=x(1-t²)dt; .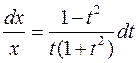

Маємо рівняння з відокремленими змінними відносно х і t. Інтегруючи, знаходимо загальний розв’язок цього рівняння

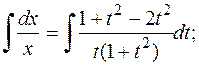
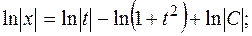
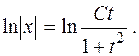
Потенціюючи, знаходимо x=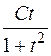, або x(1+t²)=Ct.

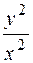Якщо у=хt, то . Отже, x(1+ )=C,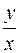

або x²+y²= Cy - загальний інтеграл даного рівняння.

Беручи до уваги початкові дані у(1)=1, маємо:

1+1=С×1, отже С=2.

Таким чином,

х²+у² =2у – частинний розв’язок даного рівняння.

б) Дане рівняння є диференційним лінійним рівнянням першого порядку, тому що воно містить шукану функцію у та її похідну у′ в першому степені і має вигляд:

y′+p(x)y=q(x).

Розв’язок шукаємо у вигляді у=UV, де U та V – деякі невідомі функції аргументу х.

Якщо у = UV, то y′ = U′V+UV′ і дане рівняння матиме вигляд

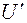V+U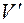-UVtgx = 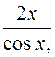, (11.17)

або

V(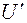-Utgx)+UV¢=.

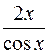Обираємо функцію U таким чином, щоб вираз у дужках дорівнював нулю, тобто

U′-Utgx=0 (11. 18)

тоді

UV′=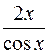 . (11.19)

Рівняння (11.18) - є рівняння з відокремлюваними змінними відносно U та х.

Розв’яжемо це рівняння:

; .

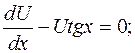
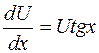Інтегруючи, маємо:

lnU=-ln cosx.

Отже,

U=- частинний розв’язок рівняння (11.18).

Знайдену функцію U підставляємо в (11.19). Отже,

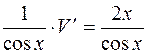; V′=2x;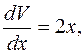

dV = 2xdx.

Інтегруючи, маємо V = x²+C – загальний розв’язок рівняння (11.19).

Таким чином, y = 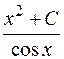- загальний розв’язок даного рівняння.

Беручи до уваги початкові дані у(0) = 1, маємо 1=,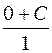

отже С=1.

Таким чином, y= - частинний розв’язок даного рівняння. ◄

2.Знайти частинні розв’язки диференціальних рівнянь, що задовольняють початковим умовам:

а)y′′-3y′+2y=0; y(0)=0; y′(0)=1.

б)y''-4y'+4y=0; y(0)=0; y'(0)=2.

в)y''+4y'+5y=0; y(0)=2; y'(0)=0.

► а) Дане рівняння є лінійним однорідним рівнянням другого порядку зі сталими коефіцієнтами. Складемо характеристичне рівняння:

K² -3K+2=0 , коренями якого є: K₁=1, K₂ = 2 - дійсні і різні. Загальний розв’язок цього рівняння має вигляд:

y=C₁e^x+C₂e^2x.

Знайдемо частинний розв’язок, що задовольняє початковим умовам. Похідна від загального розв’язку y′=C₁e^x+2C₂e^2x.

Підставляючи у загальний розв’язок замість х, у та у′ відповідні значення за умовою, маємо

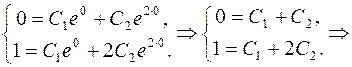
C₂=1, C₁=1_.

Отже, y= -e^x +e^2x частинний розв’язок.

б) Дане рівняння є лінійним однорідним рівнянням другого порядку зі сталими коефіцієнтами. Його характеристичне рівняння: K²-4K+4=0, корені якого K₁=K₂=2 – дійсні та рівні. Загальний розв’язок: y=C₁e^2x+C₂xe^2x.

Знайдемо частинний розв’язок, що задовольняє початковим умовам.

y′=2C₁e^2x+C₂e^2x+2C₂xe^2x.

Враховуючи значення х, у та у′, маємо:

Отже, y = 2xe^2x - частинний розв’язок.

в) Дане рівняння є лінійним однорідним рівнянням другого порядку зі сталими коефіцієнтами. Його характеристичне рівняння:

K²+4K+5=0, корені якого є комплексно спряжені числа K₁=-2+ i, K₂= -2 - i

Тому загальний розв’язок має вигляд:

y = e^-2x(C₁cosx+C₂sinx).

Знайдемо частинний розв’язок, враховуючи початкові значення х, у та у′.

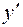=-2e^-2x(C₁cosx+C₂sinx)+e^-2x(-C₁sinx+C₂cosx).

Маємо:

.

Отже,

y=e^-2x(2cosx+4sinx) -частинний розв’язок. ◄

3. Знайти частинний розв’язок диференціального рівняння

,

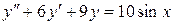що задовольняє початковим умовам ; .

► Маємо лінійне неоднорідне диференціальне рівняння другого порядку з постійними коефіцієнтами. Відомо, що загальний розв’язок такого рівняння складається з суми загального розв’язку відповідного однорідного рівняння і частинного розв’язку неоднорідного рівняння, тобто

.
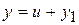