Лабораторная работа 4
Непрерывные отображения
Примеры решения задач
Задача 1 Является ли заданное отображение 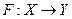 на своей естественной области
на своей естественной области
определения непрерывным в точке x0?
Пример 1  ,
, 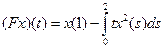 , x0(t) = t.
, x0(t) = t.
Решение. Очевидно, что заданное отображение определено на всем C[0;2]. Представим его в виде: Fx = F1x – F2x, где F1x = x(1), 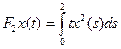 , и покажем, что F1 и F2 непрерывны в любой точке x0
, и покажем, что F1 и F2 непрерывны в любой точке x0  C[0;2]. Пусть последовательность (xn) сходится к x0 в C[0;2]. Тогда
C[0;2]. Пусть последовательность (xn) сходится к x0 в C[0;2]. Тогда
ρL1(F1xn, F1x0)= dt ≤
dt ≤  |xn(t) - x0(t)| = ρc(xn, x0)
|xn(t) - x0(t)| = ρc(xn, x0)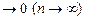 .
.
Отсюда следует, что F1 непрерывно.
Докажем непрерывность F2. Так как функция x0  C[0;2], то она ограничена на [0;2], т. е.
C[0;2], то она ограничена на [0;2], т. е.  M
M  R: |x0(s)| ≤ M
R: |x0(s)| ≤ M  s
s  [0;2]. А так как xn
[0;2]. А так как xn x0 равномерно на [0;2], то, начиная с некоторого номера |xn(s)| ≤ 2M на [0;2] (почему?). Тогда
x0 равномерно на [0;2], то, начиная с некоторого номера |xn(s)| ≤ 2M на [0;2] (почему?). Тогда
ρL1(F2xn, F2x0) =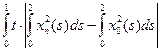 dt =
dt =  =
=
= ≤
≤ 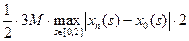 =
=
=3M ρc(xn, x0)
ρc(xn, x0)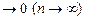 .
.
Отсюда следует, что F2 xn F2 x0 в L1[0;1]. Поэтому в силу произвольности х0 отображение F непрерывно в любой точке из C[0;2].
F2 x0 в L1[0;1]. Поэтому в силу произвольности х0 отображение F непрерывно в любой точке из C[0;2].
Пример 2 F: L2[0;1]  L1[0;1], (Fx)(t) = tx(t3), x0 = 0.
L1[0;1], (Fx)(t) = tx(t3), x0 = 0.
Решение. Пусть последовательность (xn) сходится к x0 в L2[0;1]. Заметим, что
ρL2(xn,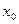 ) =
) =  =
=  .
.
Теперь в силу неравенства Коши-Буняковского
ρL1(Fxn, Fx0)=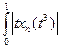 dt =
dt = 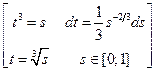 =
=  dt ≤
dt ≤
≤  ρL2(xn,
ρL2(xn,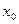 )
)
(аналогичные вычисления показывают, что Fх принадлежит L1[0;1] при х из L2[0;1]; поэтому отображение F определено на всем L1[0;1]). Значит, F – непрерывное отображение в точке 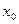 .
.
Пример 3 F: L1[0;1] → L2[0;1], (Fx)(t) = 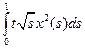 , x0 = 0.
, x0 = 0.
Решение. Покажем, что отображение не является непрерывным. Возьмём последовательность xn = 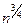 .
. 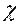 [0;1/n], которая
[0;1/n], которая  0 в L1[0;1] (действительно,
0 в L1[0;1] (действительно,
ρL1(xn,0)=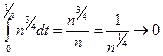 при
при 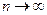 ).
).
Рассмотрим теперь выражение
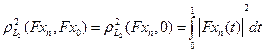 =
= = =
= = ==
==  =
=  =
=  .
.
Следовательно, последовательность ρL2(Fxn, Fx0) не стремится к нулю при 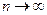 , а потому Fxn не стремится к Fx0.
, а потому Fxn не стремится к Fx0.
Пример 4 F: L2[0;1] → L1[0;1], (Fx)(t) =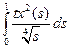 , x0 = 0.
, x0 = 0.
Решение. Покажем, что отображение не является непрерывным. Заметим, что
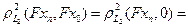
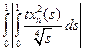 dt =
dt = 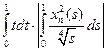 =
= 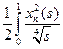 ds.
ds.
Возьмем последовательность xn =  .
. 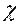 [0;1/ n-2], которая → 0 в L2[0;1], так как
[0;1/ n-2], которая → 0 в L2[0;1], так как 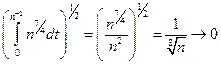 при n → ∞.
при n → ∞.
Тогда
ρL1(Fxn,0) =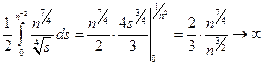 при n→ ∞,
при n→ ∞,
а потому Fxn не стремится к Fx0.
Задача 2 Является ли заданное отображение 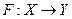 : а) непрерывным; б) равномерно
: а) непрерывным; б) равномерно
непрерывным; в) удовлетворяющим условию Липшица?
Пример 1 X = Y = C[-4;2], (Fx)(t) = x(t)sin x(t).
Решение. а) Отображение F является непрерывным, так как
ρ(Fx,Fx0) = 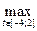 |x(t)sin x(t) - x0(t)sin x0(t)| ≤
|x(t)sin x(t) - x0(t)sin x0(t)| ≤ 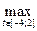 |x(t)sin x(t) - x0(t)sin x(t)| +
|x(t)sin x(t) - x0(t)sin x(t)| +
+ |x0(t)sin x(t) - x0(t)sin x0(t)| ≤ 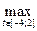 |x(t) - x0(t)| +
|x(t) - x0(t)| +
+ 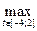 |x0(t)
|x0(t) 2sin
2sin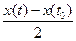 ·cos
·cos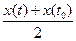 )| ≤
)| ≤ 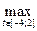 |x(t) - x0(t)| + M
|x(t) - x0(t)| + M
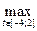 |x(t) - x0(t)| =
|x(t) - x0(t)| =
= (M+1)ρ(x,x0)
(здесь M =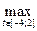 | x0(t) |; мы воспользовались неравенством
| x0(t) |; мы воспользовались неравенством 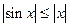 ).
).
б) Покажем, что F не является равномерно непрерывным. Возьмём
xn(t) = 2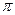
 , yn(t)=
, yn(t)=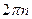 . Тогда ρ(xn,yn)=
. Тогда ρ(xn,yn)=  → 0 при n→ ∞, но
→ 0 при n→ ∞, но
ρ(Fxn, Fyn)= 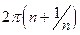 sin
sin -
- 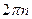
 sin
sin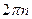 =
= 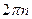 sin
sin +
+ sin
sin = =
= = ,
,
а значит, ρ(Fxn, Fyn) не стремится к нулю при n→ ∞. Это противоречит определению равномерной непрерывности (проверьте).
в) Так как F не является равномерно непрерывным, то оно не удовлетворяет условию Липшица (почему?).
Пример 2 X = l2, Y = l∞ , Fx =  .
.
Решение. Покажем, что F удовлетворяет условию Липшица с константой L=1. Заметим, что
ρl∞(Fx, Fy) =  {
{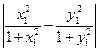 ; | x1 - y1 |; | x1 - y1 |; …}.
; | x1 - y1 |; | x1 - y1 |; …}.
Обозначим f(x) =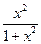 . Тогда
. Тогда
|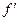 (x)| =
(x)| = =
= .
.
Следовательно, по теореме Лагранжа | f(x1) - f(y1) | ≤ | x1 - y1 |, а значит,
ρl∞(Fx, Fy) =  {
{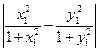 ; | x1 - y1 |; | x1 - y1 |; …} ≤
; | x1 - y1 |; | x1 - y1 |; …} ≤  | xk - yk | ≤ ρl2(x,y).
| xk - yk | ≤ ρl2(x,y).
Так как F удовлетворяет условию Липшица, то оно равномерно непрерывно, а потому и непрерывно.
Пример 3 X = L1[0;1], Y = L2[-1;1], (Fx)(t)=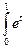 arctgx(s)ds.
arctgx(s)ds.
Решение. Покажем, что F удовлетворяет условию Липшица. Действительно,
ρL2(Fx, Fy) = =
=  =
=
= 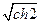
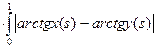 ds.
ds.
Так как 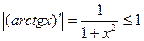 , то по теореме Лагранжа
, то по теореме Лагранжа  . Поэтому при любых х,у
. Поэтому при любых х,у
ρL2(Fx, Fy) 
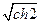 ρL1(x,y).
ρL1(x,y).
Так как F удовлетворяет условию Липшица, то оно является равномерно непрерывным.
Пример 4 X=l2 Y=l1 , Fx= .
.
Решение. а) Покажем, что F непрерывно. Действительно, если xn → x0 в l2, то чис-ловая последовательность xn(21) сходится к x0(21). Тогда
ρl2(Fxn, Fx0) = 0 при n→ ∞.
0 при n→ ∞.
б) Покажем, что F не является равномерно непрерывным. Пусть
xn(21) =  , yn(21) = n, xn (k) = yn (k) = 0
, yn(21) = n, xn (k) = yn (k) = 0 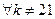 .
.
Тогда
ρl2(xn,yn) = при n→ ∞,
при n→ ∞,
но
ρl1(Fxn,Fyn) =  при n→ ∞.
при n→ ∞.
в) Так как F не является равномерно непрерывным, то оно не удовлетворяет и условию Липшица.
Задания лабораторной работы
Задача 1 Выяснить, является ли заданное отображение 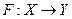 на своей естественной
на своей естественной
области определения непрерывным в точке x0?
| № | X | Y | F | x0(t) |
| 1.1 | L2[0;1] | L1[0;1] | (Fx)(t) = 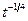 sin x(t) sin x(t)
| t2 |
| 1.2 | C[0;1] | L1[0;1] | (Fx)(t) =sin x2(t) | t |
| 1.3 | L2[0;1] | L2[0;1] | (Fx)(t) = x(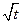 ) )
| 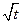
|
| 1.4 | C[0;1] | C[0;1] |
(Fx)(t) = ∫t|x(s)|/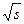 ds
0 ds
0
| t |
| 1.5 | C[0;1] | C[0;2] | (Fx)(t) = 2x3(t/2) | |
| 1.6 | L1[0;1] | L2[0;1] | (Fx)(t) = x(t) |
Задача 2 Является ли заданное отображение 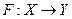 : а) непрерывным; б) равномерно
: а) непрерывным; б) равномерно
непрерывным; в) удовлетворяющим условию Липшица?
| № | X | Y | F |
| 2.1 | C[0;1] | C[0;1] | (Fx)(t) =x2(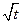 )et )et
|
| 2.2 | C[-1;1] | C[-1;1] | (Fx)(t) =x(t)/(1+x2(t)) |
| 2.3 | L2[-1;0] | L1[-1;0] | (Fx)(t) =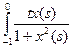 ds ds
|
| 2.4 | C[-1;2] | L1[-1;2] | (Fx)(t) =
|
| 2.5 | l1 | l1 | Fx = (cosx (1), x (2), x (3),…, x(k),…) |
| 2.6 | C[-5;2] | L1[-5;2] | Fx(t) =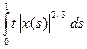
|