Сложение и умножение вероятностей
Т: Если 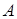 и
и  - несовместные события
- несовместные события 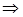
 , (13.3)
, (13.3)
в противном случае
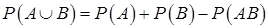 . (13.4)
. (13.4)
Формула (13.4) справедлива и для вероятности суммы  несовместных событий.
несовместных событий.
Следствие. Вероятность противоположного событию 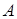 события
события 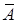 равна
равна  . Из (13.3)
. Из (13.3) 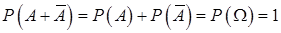 .
.
Примеры.
1. В урне 2 зелёных, 4 жёлтых, 7 красных, 10 белых шаров. Вынимают один шар. Найти вероятность того, что он не белый.
Решение. Пространство 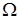 содержит 23 элементарных события. Случайное событие, состоящее в выборе цветного шара
содержит 23 элементарных события. Случайное событие, состоящее в выборе цветного шара 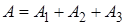 . Здесь
. Здесь  - событие, состоящее в выборе зелёного шара,
- событие, состоящее в выборе зелёного шара, 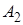 - жёлтого,
- жёлтого,  - красного. Так как
- красного. Так как 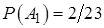 ,
,  ,
,  , по формуле (13.3) имеем
, по формуле (13.3) имеем 
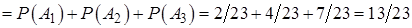 .
.
2. Вероятность того, что день пасмурный 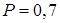 . Найти вероятность того, что день ясный.
. Найти вероятность того, что день ясный.
Решение. Событие 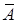 , состоящее в том, что день ясный, противоположное событию
, состоящее в том, что день ясный, противоположное событию 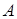 (день пасмурный), т.е.
(день пасмурный), т.е. 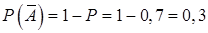 .
.
О: Вероятность события 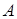 в предположении, что произошло событие
в предположении, что произошло событие  , называется условной вероятностью и обозначается
, называется условной вероятностью и обозначается  . События
. События 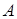 и
и  называются независимыми, если предположение о том, что произошло одно из них, не влияет на вероятность другого, т.е.
называются независимыми, если предположение о том, что произошло одно из них, не влияет на вероятность другого, т.е.
 ,
,  . (13.5)
. (13.5)
Т: Вероятность  совместного наступления событий
совместного наступления событий 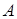 и
и  вычисляется по формуле
вычисляется по формуле
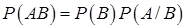 (13.6)
(13.6)
Если события 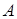 и
и  независимы, то
независимы, то
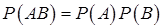 . (13.7)
. (13.7)
Эта формула справедлива и для вероятности произведения  независимых событий.
независимых событий.
Примеры.
1). Из урны, содержащей 3 белых и 7 чёрных шаров, вынимают два. Какова вероятность того, что оба шара белые?
Решение. Событие 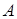 - вынут белый шар,
- вынут белый шар, 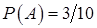 . Событие
. Событие  - вынут второй белый шар при условии, что произошло
- вынут второй белый шар при условии, что произошло 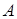 ,
,  , тогда вероятность того, что оба шара белые
, тогда вероятность того, что оба шара белые 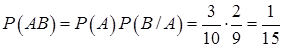 .
.
2. Рабочий обслуживает три станка, работающих независимо друг от друга. Вероятность того, что в течение часа станок не потребует внимания рабочего для первого станка  , для второго
, для второго 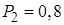 , для третьего
, для третьего 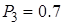 . Найти вероятность того, что в течение часа ни один станок не потребует внимания рабочего.
. Найти вероятность того, что в течение часа ни один станок не потребует внимания рабочего.
Решение. По формуле (10.7) имеем 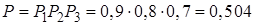 .
.
Т: пусть случайные события 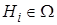 ,
, 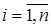 образуют полную группу событий. Тогда для любого случайного события
образуют полную группу событий. Тогда для любого случайного события 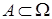 справедлива формула
справедлива формула
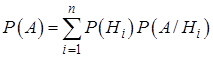 . (13.8)
. (13.8)
Эту формулу называют формулой полной вероятности.
Пример. Имеется два ящика с шарами. В первом ящике два белых и один чёрный шар, во втором ящике один белый и четыре чёрных шара. Наугад выбираем ящик и вынимаем шар. Какова вероятность того, что он белый?
Решение. Пространство 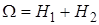 , где
, где 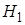 - выбор первого ящика,
- выбор первого ящика, 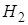 - второго, событие
- второго, событие 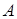 - выбор шара, тогда
- выбор шара, тогда 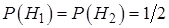 ,
,  ,
,  и по формуле (13.8)
и по формуле (13.8) 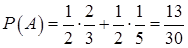 .
.
Из формулы 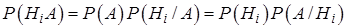 и (13.8) получается так называемая формула Байеса
и (13.8) получается так называемая формула Байеса
 ,
, 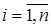 . (13.9)
. (13.9)
Формула трактуется следующим образом: имеется полная группа гипотез 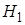 , …,
, …, 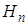 , вероятности которых известны до опыта. Проводится опыт, в результате которого может наступить или не наступить событие
, вероятности которых известны до опыта. Проводится опыт, в результате которого может наступить или не наступить событие 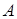 . Если событие
. Если событие 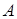 наступило, то (13.9) определяет вероятности гипотез после опыта.
наступило, то (13.9) определяет вероятности гипотез после опыта.