Элементы математической статистики
Опорный конспект
15.1. Основные понятия математической статистики.
О: Выборка 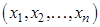 -совокупность значений СВ -совокупность значений СВ  , полученных в результате , полученных в результате  независимых экспериментов.
О: Статистический ряд: независимых экспериментов.
О: Статистический ряд:
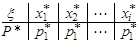 , , , ,
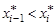 , ,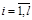 , , -относительная частота, -относительная частота,  -частота появления -частота появления 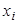 .
О: Статистический ряд по интервалам .
О: Статистический ряд по интервалам
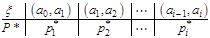
 -число значений СВ -число значений СВ  ,
попавших в ,
попавших в  . Графическое изображение . Графическое изображение
 О
О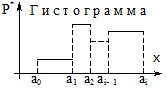 : Эмпирическая функция распределения: : Эмпирическая функция распределения:
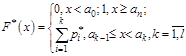
| 15.2. Определение неизвестных параметров распределения
О: Для выборки среднее арифметическое  ,дисперсия ,дисперсия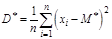 ; для статистического ряда: ; для статистического ряда:  , , ; ;
 , , 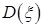 -числовые
характеристики СВ -числовые
характеристики СВ  с выборкой с выборкой 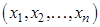   , ,  .
О: Доверительный интервал .
О: Доверительный интервал 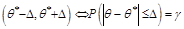 , , 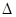 - точность оценки - точность оценки  параметра параметра  в функции распределения в функции распределения СВ СВ  , ,  -коэффициент доверия.
Для нормального распределения с параметрами -коэффициент доверия.
Для нормального распределения с параметрами 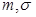 при при 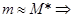  . Для двумерной СВ . Для двумерной СВ  с выборкой с выборкой
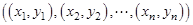 выборочный коэффициент корреляции выборочный коэффициент корреляции

 . .
|
Основные понятия математической статистики
Построение эмпирических законов распределения
Математическая статистика – наука о методах обработки экспериментальных данных, полученных при изучении закономерностей в случайных массовых явлениях. Способ статистической обработки, равно как и ценность её результатов полностью зависит от положенной в основу вероятностной модели, которая должна объяснить вероятностную структуру наблюдений.
Пусть произведено  независимых экспериментов и получено
независимых экспериментов и получено  значений
значений 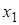 ,
, 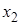 ,…,
,…,  случайной величины
случайной величины 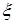 .
.
О: Генеральной совокупностью называется множество всех возможных значений случайной величины 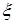 . Выборкой объёма
. Выборкой объёма 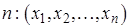 называется совокупность значений
называется совокупность значений 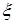 , полученных в результате
, полученных в результате  независимых экспериментов.
независимых экспериментов.
По исследованию выборки необходимо сделать правильный вывод о СВ 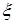 . Например, по толщине покрытия 100 деталей из серии необходимо сделать вывод о качестве покрытия деталей. В этом случае классическую вероятность заменяют статистической.
. Например, по толщине покрытия 100 деталей из серии необходимо сделать вывод о качестве покрытия деталей. В этом случае классическую вероятность заменяют статистической.
О: Статистическим рядом называется таблица, в которой записываются в упорядоченном по возрастанию виде различные элементы выборки  ,
, 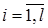 , и относительные частоты
, и относительные частоты  (
( - частота появления
- частота появления 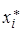 ):
):
 ,
,  . (15.1)
. (15.1)
При большом числе измерений анализ такого материала затруднителен. Поэтому поступают следующим образом.
Составляется статистический ряд по интервалам или вариационный ряд. Весь интервал полученных значений величины 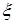 разбивается на интервалы
разбивается на интервалы 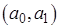 ,
,  ,…,
,…,  , подсчитываются относительные частоты
, подсчитываются относительные частоты  , где
, где  - число значений величины
- число значений величины 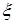 , попавших в
, попавших в  , и строится таблица:
, и строится таблица:
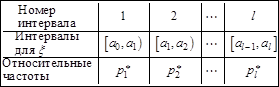 (15.2 )
(15.2 )
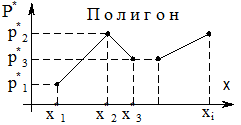
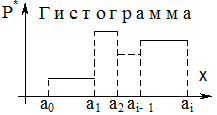
Графическими изображениями статистических рядов являются полигон и гистограмма.
Полигон состоит из отрезков, соединяющих точки 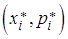 ,
, 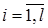 , где в случае ряда по интервалам
, где в случае ряда по интервалам 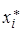 - срединное значение интервала
- срединное значение интервала 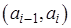 (рис. 15.1)
(рис. 15.1)
| 
| |
| Рис 15.1. | Рис. 15.2. |
Гистограмма служит для изображения интервального статистического ряда (15.2). По оси 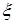 откладывают интервалы
откладывают интервалы 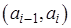 ,
, 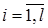 варьирования СВ
варьирования СВ 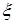 и на этих отрезках строят прямоугольники с высотами
и на этих отрезках строят прямоугольники с высотами  (рис. 15.2).
(рис. 15.2).
О: Эмпирической функцией распределения СВ 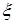 , для которой составлен статистический ряд (15.2), называется
, для которой составлен статистический ряд (15.2), называется 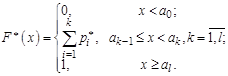
При малых  ,
, 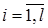 и больших
и больших  функция
функция 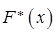 близка к теоретической функции распределения
близка к теоретической функции распределения 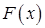 .
.
Определение неизвестных параметров распределения
и выборочного коэффициента корреляции
Выборочные числовые характеристики. Оценки параметров
Для выборки 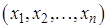 СВ
СВ 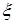 и для статистического ряда определяются следующие числовые характеристики.
и для статистического ряда определяются следующие числовые характеристики.
О: Среднее арифметическое выборки 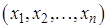 это
это  ,
,
среднее арифметическое статистического ряда (15.1):  . Дисперсия выборки
. Дисперсия выборки 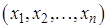 это
это  ,
,
дисперсия статистического ряда (15.1) ‑ 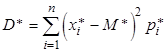 .
.
Среднее квадратичное отклонение: 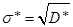 .
.
Пусть 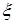 случайная величина с функцией распределения
случайная величина с функцией распределения  , где
, где 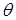 - неизвестный параметр распределения, т.е. неизвестная числовая характеристика СВ
- неизвестный параметр распределения, т.е. неизвестная числовая характеристика СВ 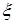 . Например,
. Например, 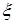 имеет нормальное распределение с неизвестным параметром
имеет нормальное распределение с неизвестным параметром 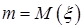 . Рассмотрим
. Рассмотрим  выборок
выборок 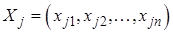 ,
,  , этой СВ
, этой СВ 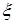 . Обозначим через
. Обозначим через  оценку величины
оценку величины 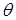 , её можно представить как случайную величину, зависящую от
, её можно представить как случайную величину, зависящую от 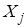 ,
,  , т.е.
, т.е.  . Чтобы выбрать в некотором смысле лучшую оценку
. Чтобы выбрать в некотором смысле лучшую оценку  , рассматриваются свойства оценок: несмещённость, состоятельность, эффективность.
, рассматриваются свойства оценок: несмещённость, состоятельность, эффективность.
О: Оценка  параметра
параметра 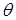 называется несмещённой, если её математическое ожидание
называется несмещённой, если её математическое ожидание 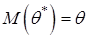 , состоятельной, если
, состоятельной, если  по вероятности сходится к
по вероятности сходится к 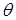 при
при 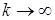 , т.е.
, т.е.  . Несмещённая оценка
. Несмещённая оценка  называется эффективной, если её дисперсия
называется эффективной, если её дисперсия  - наименьшая среди всех дисперсий, вычисляемых для оценок
- наименьшая среди всех дисперсий, вычисляемых для оценок  по выборкам одинакового объёма.
по выборкам одинакового объёма.
Т: Среднее арифметическое  выборки
выборки 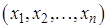 СВ
СВ 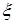 , имеющей математическое ожидание
, имеющей математическое ожидание  и дисперсию
и дисперсию  , является несмещённой и состоятельной оценкой математического ожидания. В случае нормального распределения СВ
, является несмещённой и состоятельной оценкой математического ожидания. В случае нормального распределения СВ 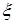 эта оценка является эффективной.
эта оценка является эффективной.
Пример. Найти параметры распределения СВ 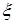 в примере п. 15.1, если
в примере п. 15.1, если 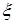 имеет нормальный закон распределения.
имеет нормальный закон распределения.
Решение. Плотность вероятности для нормального закона распределения 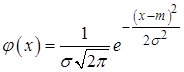 , неизвестные параметры -
, неизвестные параметры -  ,
, 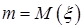 . Т.к.
. Т.к. 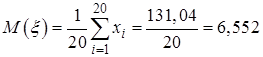 (мкм),
(мкм),
 (мкм2), то
(мкм2), то 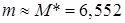 ,
,  .
.
Доверительные интервалы параметров
Рассмотренные выше оценки параметров являются точечными. При малом объёме выборки, чтобы избежать грубых ошибок, вводят интервальную оценку. Обозначим точность оценки  параметра
параметра 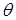 через
через  , т.е.
, т.е. 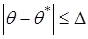 , а через
, а через 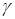 - вероятность
- вероятность  , т.е.
, т.е. 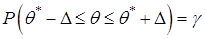 . Последнее условие означает, что интервал
. Последнее условие означает, что интервал 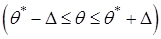 покрывает значение
покрывает значение 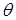 с заданной вероятностью
с заданной вероятностью 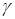 . Он называется доверительным интервалом,
. Он называется доверительным интервалом, 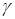 - коэффициентом доверия. На практике
- коэффициентом доверия. На практике 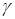 выбирают достаточно близким к 1.
выбирают достаточно близким к 1.
Величины 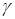 ,
,  и объём выборки связаны между собой. Если определены две из них, то можно определить третью.
и объём выборки связаны между собой. Если определены две из них, то можно определить третью.
Пусть случайная величина 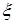 имеет нормальное распределение с параметрами
имеет нормальное распределение с параметрами 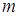 ,
,  .
.
В качестве оценки 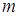 берётся
берётся 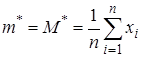 . Все элементы
. Все элементы 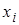 ,
, 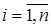 , выборки случайные и имеют то же распределение, что и
, выборки случайные и имеют то же распределение, что и 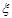 с параметрами
с параметрами  ,
, 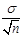 . Тогда по (15.6) в силу нечётности функции Лапласа
. Тогда по (15.6) в силу нечётности функции Лапласа  :
:
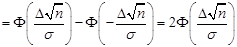 .
.
Обозначим 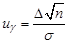 , тогда
, тогда 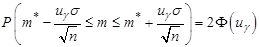 .
.
Если 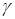 задано, то
задано, то  находится по таблице функции Лапласа. Интервал
находится по таблице функции Лапласа. Интервал  с вероятностью
с вероятностью 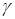 покрывает значение
покрывает значение 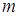 и является доверительным для
и является доверительным для 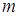 . При этом предполагается, что
. При этом предполагается, что  известно. Если
известно. Если  заменить приближённым значением
заменить приближённым значением  , то коэффициент доверия
, то коэффициент доверия 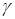 уменьшится.
уменьшится.
Пример. Найти доверительный интервал с коэффициентом доверия 0,95 для 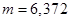 и
и  .
.
Решение. По таблице Лапласа  . Так как
. Так как  ,
, 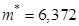 , то имеем
, то имеем 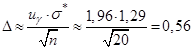 , доверительный интервал
, доверительный интервал  и
и 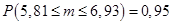 .
.
Выборочный коэффициент корреляции
Пусть проведено  независимых испытаний, в результате которых получены выборочные значения двумерной СВ
независимых испытаний, в результате которых получены выборочные значения двумерной СВ  : (
: ( ,
,  , …,
, …,  ).
).
Аналогично случаю одномерной СВ 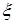 определяются выборочные числовые характеристики:
определяются выборочные числовые характеристики: 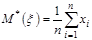 ,
,  ,
,  ,
, 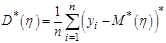 ,
, 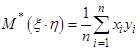 .
.
О: Выборочным коэффициентом корреляции СВ 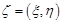 называется
называется 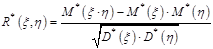 .
.
Пример. Дана выборка СВ  :(2,2), (4,5), (6,7), (8,10). Найти
:(2,2), (4,5), (6,7), (8,10). Найти  .
.
Решение.  ,
,  ,
, 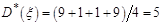 ,
, 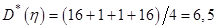 ,
, 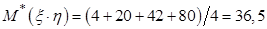 ,
,  . Коэффициент корреляции близок к 1, т.е. зависимость между
. Коэффициент корреляции близок к 1, т.е. зависимость между  ,
, 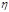 близка к линейной.
близка к линейной.